Mathematics
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Circles
4 Likes
Answer
From figure,
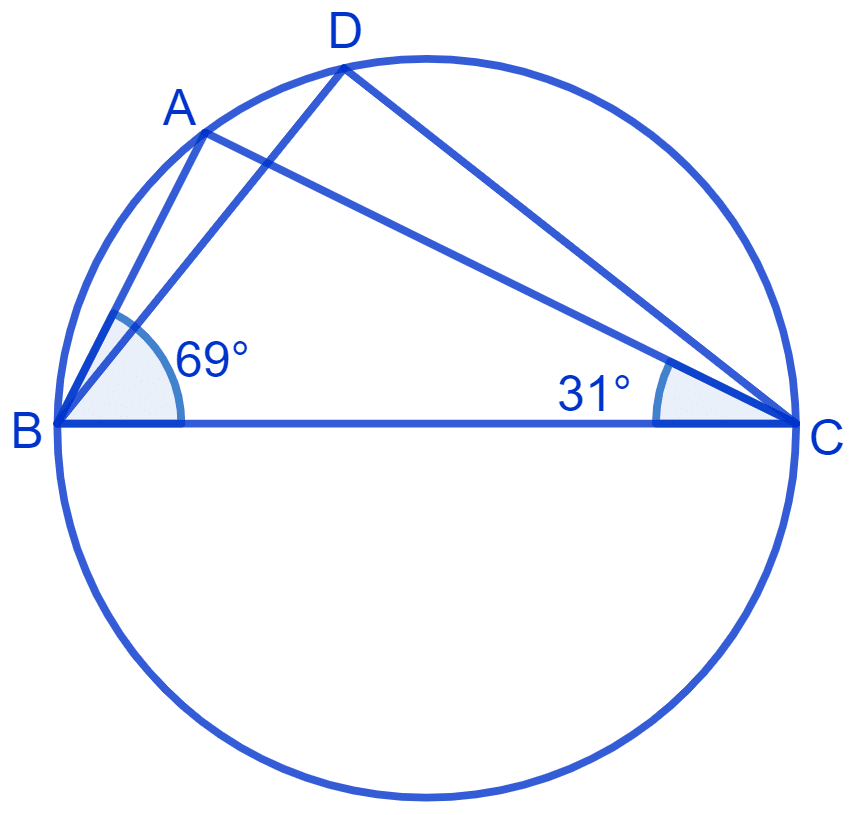
There is a circle with center O and chord AB which is equal to radius of the circle.
In ∆ AOB,
⇒ OA = OB = AB
∴ ∆ OAB is an equilateral triangle.
⇒ ∠AOB = 60° (Each angle of an equilateral triangle equals to 90°)
We know that,
The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.
⇒ ∠AOB = 2∠ACB
⇒ ∠ACB = ∠AOB
⇒ ∠ACB = x 60° = 30°
⇒ ∠ACB = 30°.
Since, ACBD is a cyclic quadrilateral
⇒ ∠C + ∠D = 180° (Opposite angles of cyclic quadrilateral are supplementary)
⇒ 30° + ∠D = 180°
⇒ ∠D = 180° - 30°
⇒ ∠D = 150°.
Hence, angle subtended on minor arc equals to 150° and angle subtended on major arc equals 30°.
Answered By
2 Likes
Related Questions
A circular park of radius 20 m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
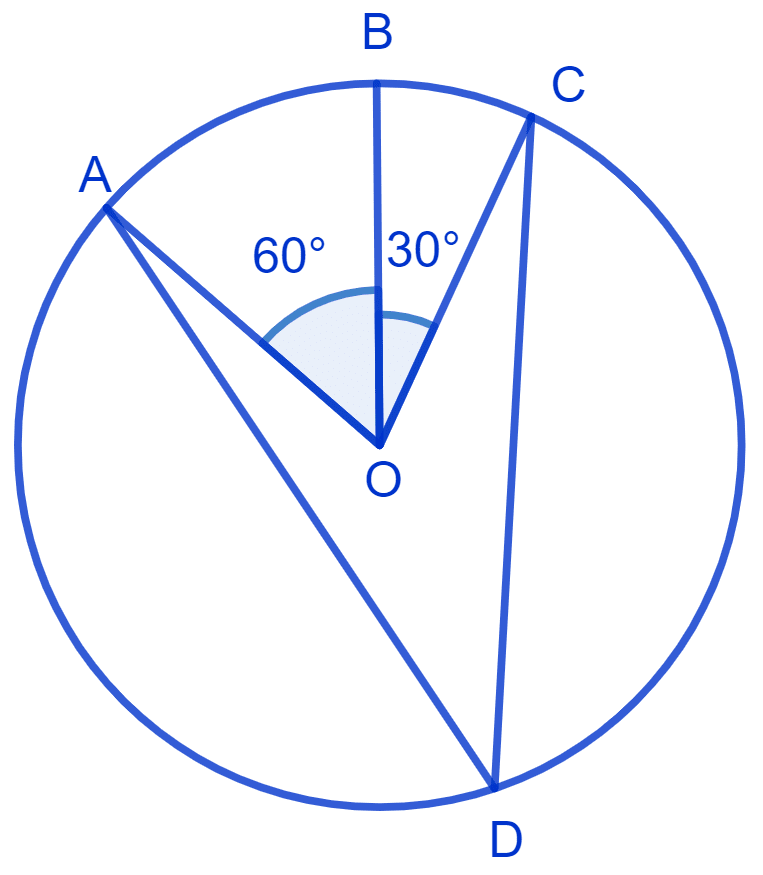
In Fig. A, B and C are three points on a circle with centre O such that ∠BOC = 30° and ∠AOB = 60°. If D is a point on the circle other than the arc ABC, find ∠ADC.
In Fig. ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.
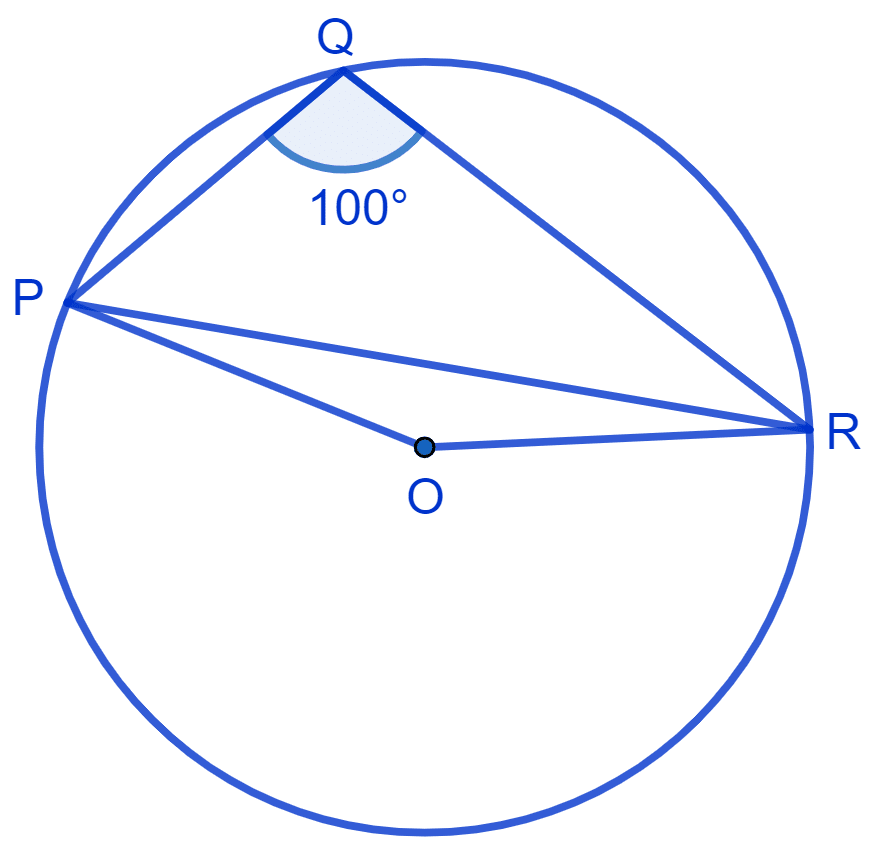
In Fig. ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.