KnowledgeBoat Logo

Physics

A cell of emf 1.8 V and internal resistance 2 Ω is connected in series with an ammeter of resistance 0.7 Ω and resistance of 4.5 Ω as shown in figure.

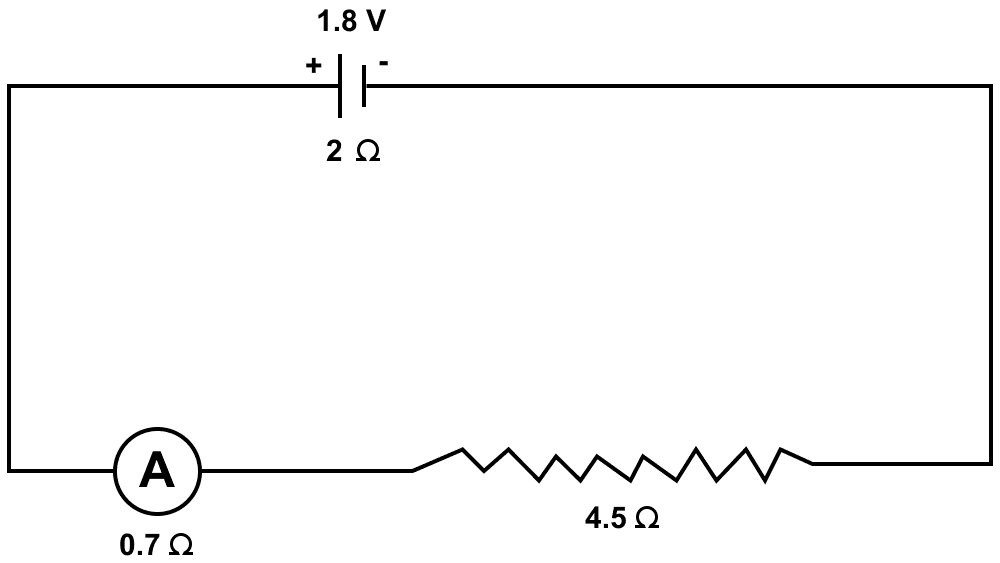
A cell of emf 1.8 V and internal resistance 2 Ω is connected in series with an ammeter of resistance 0.7 Ω and resistance of 4.5 Ω as shown in figure. Current Electricity, Concise Physics Solutions ICSE Class 10.

(a) What would be the reading of the ammeter?

(b) What is the potential difference across the terminals of the cell ?

Current Electricity

54 Likes

Answer

(a) Given,

e.m.f. (ε) = 1.8 V

Internal resistance (r) = 2 Ω

I = ?

Total resistance of arrangement = 2 + 0.7 + 4.5 = 7.2 Ω

From relation,

I=εRI = \dfrac{ε}{R}

Substituting the values in the formula above we get,

I=1.87.2I=0.25AI = \dfrac{1.8}{7.2} \\[0.5em] I = 0.25 A \\[0.5em]

Hence, reading of ammeter = 0.25 A

(b) Current (I) = 0.25 A

total resistance (excluding internal resistance) = 4.5 + 0.7 = 5.2 ohm

Using ohm's law

V = IR

Substituting the values in the formula above we get,

V = 0.25 × 5.2

V = 1.3 V

Hence, potential difference across the terminals of the battery = 1.3 V

Answered By

39 Likes

Related Questions