KnowledgeBoat Logo

Mathematics

(-2, 4), (4, 8), (10, 7) and (11, -5) are the vertices of a quadrilateral. Show that the quadrilateral, obtained on joining the mid-points of its sides, is a parallelogram.

Straight Line Eq

15 Likes

Answer

Let the given points be A(-2, 4), B(4, 8), C(10, 7) and D(11, -5).

And, let P, Q, R and S be the mid-points of AB, BC, CD and DA respectively.

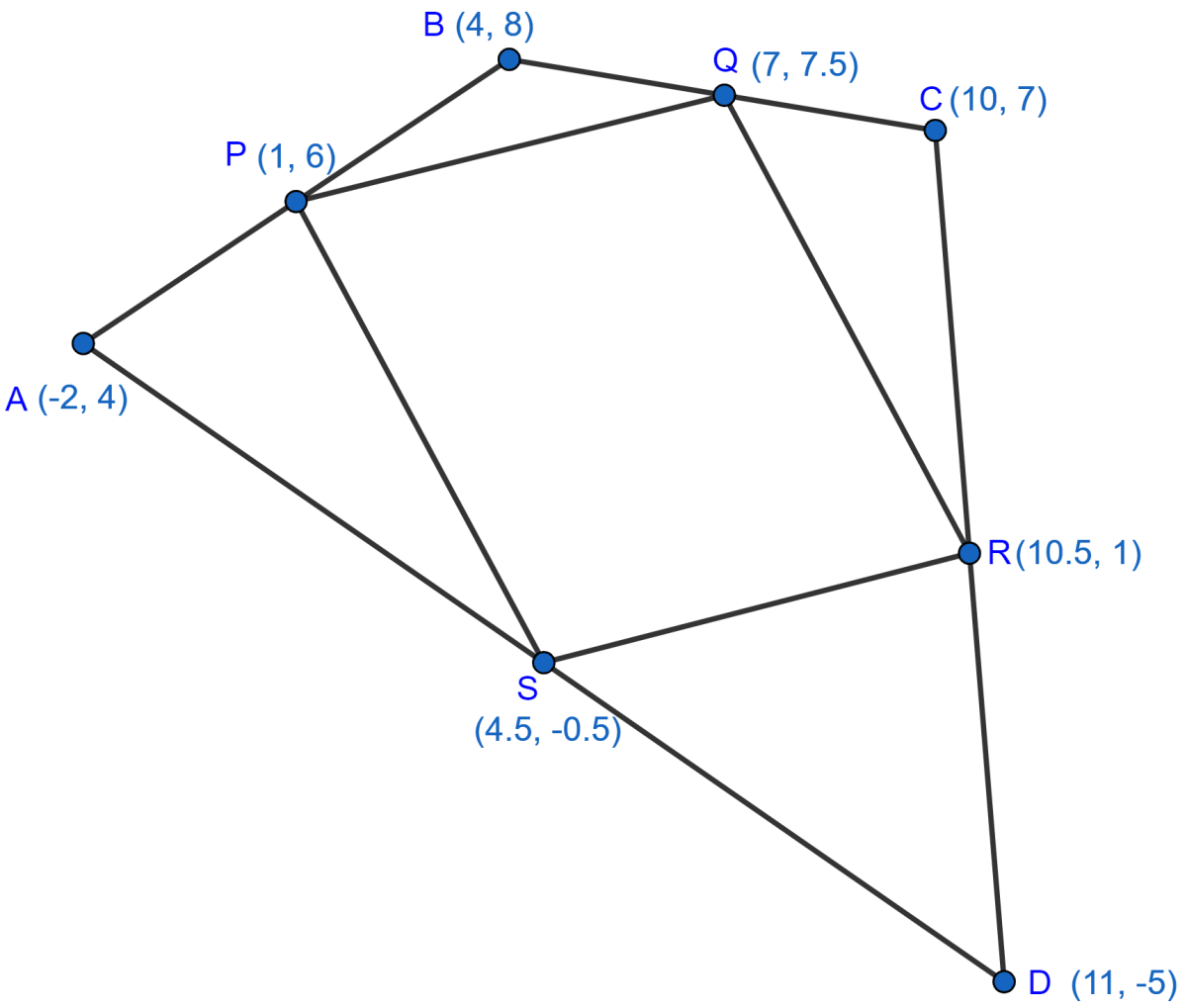
(-2, 4), (4, 8), (10, 7) and (11, -5) are the vertices of a quadrilateral. Show that the quadrilateral, obtained on joining the mid-points of its sides, is a parallelogram. Equation of a Line, Concise Mathematics Solutions ICSE Class 10.

By mid-point formula,

Mid-point = (x1+x22,y1+y22)\Big(\dfrac{x1 + x2}{2}, \dfrac{y1 + y2}{2}\Big).

So,

⇒P=(−2+42,4+82)=(22,122)=(1,6).⇒Q=(4+102,8+72)=(142,152)=(7,7.5).⇒R=(10+112,7+(−5)2)=(212,22)=(10.5,1).⇒S=(11+(−2)2,−5+42)=(4.5,−0.5).\Rightarrow P = \Big(\dfrac{-2 + 4}{2}, \dfrac{4 + 8}{2}\Big) \\[1em] = \Big(\dfrac{2}{2}, \dfrac{12}{2}\Big) = (1, 6). \\[1em] \Rightarrow Q = \Big(\dfrac{4 + 10}{2}, \dfrac{8 + 7}{2}\Big) \\[1em] = \Big(\dfrac{14}{2}, \dfrac{15}{2}\Big) = (7, 7.5). \\[1em] \Rightarrow R = \Big(\dfrac{10 + 11}{2}, \dfrac{7 + (-5)}{2}\Big) \\[1em] = \Big(\dfrac{21}{2}, \dfrac{2}{2}\Big) = (10.5, 1). \\[1em] \Rightarrow S = \Big(\dfrac{11 + (-2)}{2}, \dfrac{-5 + 4}{2}\Big) \\[1em] = (4.5, -0.5).

By formula,

Slope = y2−y1x2−x1\dfrac{y2 - y1}{x2 - x1}

⇒Slope of PQ=7.5−67−1=1.56=14.⇒Slope of QR=1−7.510.5−7=−6.53.5=−6535=−137.⇒Slope of RS=−0.5−14.5−10.5=−1.5−6=14.⇒Slope of PS=−0.5−64.5−1=−6.53.5=−6535=−137.\Rightarrow \text{Slope of PQ} = \dfrac{7.5 - 6}{7 - 1} \\[1em] = \dfrac{1.5}{6} \\[1em] = \dfrac{1}{4}. \\[1em] \Rightarrow \text{Slope of QR} = \dfrac{1 - 7.5}{10.5 - 7} \\[1em] = \dfrac{-6.5}{3.5} \\[1em] = -\dfrac{65}{35} = -\dfrac{13}{7}. \\[1em] \Rightarrow \text{Slope of RS} = \dfrac{-0.5 - 1}{4.5 - 10.5} \\[1em] = \dfrac{-1.5}{-6} \\[1em] = \dfrac{1}{4}. \\[1em] \Rightarrow \text{Slope of PS} = \dfrac{-0.5 - 6}{4.5 - 1} \\[1em] = \dfrac{-6.5}{3.5} = -\dfrac{65}{35} \\[1em] = -\dfrac{13}{7}.

From above calculation we get,

Slope of PQ = Slope of RS and Slope of QR = Slope of PS

∴ PQ || RS and QR || PS.

Hence, proved that the quadrilateral, obtained on joining the mid-points of sides of quadrilateral with vertices (-2, 4), (4, 8), (10, 7) and (11, -5), is a parallelogram.

Answered By

8 Likes

Related Questions