Solved 2024 Question Paper ICSE Class 10 Mathematics

For an Intra-state sale, the CGST paid by a dealer to the Central government is ₹120. If the marked price of the article is ₹2000, the rate of GST is:

1. 6%

2. 10%

3. 12%

4. 16.67%

Answer

CGST% = $\dfrac{CGST}{M.P.} \times 100$

Substituting values we get :

CGST% = $\dfrac{120}{2000} \times 100$ = 6%

GST% = 2 × CGST% = 2 × 6% = 12%.

Hence, Option 3 is the correct option.

What must be subtracted from the polynomial x³ + x² - 2x + 1, so that the result is exactly divisible by (x - 3)?

1. –31

2. –30

3. 30

4. 31

Answer

Polynomial : x³ + x² - 2x + 1

Division by x - 3

⇒ x - 3 = 0

⇒ x = 3.

Let k be subtracted from the polynomial, so resulting polynomial is x³ + x² - 2x + 1 - k.

Resulting polynomial should be exactly divisible by x - 3,

Thus, substituting x = 3, in polynomial x³ + x² - 2x + 1 - k, remainder = 0.

⇒ 3³ + 3² - 2(3) + 1 - k = 0

⇒ 27 + 9 - 6 + 1 - k = 0

⇒ 31 - k = 0

⇒ k = 31.

Hence, Option 4 is the correct option.

The roots of the quadratic equation px² - qx + r = 0 are real and equal if :

(a) p² = 4qr

(b) q² = 4pr

(c) –q² = 4pr

(d) p² > 4qr

Answer

By formula,

D = b² - 4ac

For equation, px² - qx + r = 0

D = (-q)² - 4 × p × r

We know that,

Roots of a quadratic equation are real and equal if discriminant = 0.

⇒ q² - 4pr = 0

⇒ q² = 4pr.

Hence, Option 2 is the correct option.

If matrix 𝐴 = $\begin{bmatrix*}[r] 2 & 2 \\ 0 & 2 \end{bmatrix*}\text{ and } A^2 = \begin{bmatrix*}[r] 4 & x \\ 0 & 4 \end{bmatrix*}$, then the value of x is :

1. 2

2. 4

3. 8

4. 10

Answer

$\phantom{\Rightarrow} A^2 = \begin{bmatrix*}[r] 2 & 2 \\ 0 & 2 \end{bmatrix*}\begin{bmatrix*}[r] 2 & 2 \\ 0 & 2 \end{bmatrix*} \\[1em] \Rightarrow A^2 = \begin{bmatrix*}[r] 2 \times 2 + 2\times 0 & 2 \times 2 + 2 \times 2 \\ 0 \times 2 + 2 \times 0 & 0 \times 2 + 2 \times 2 \end{bmatrix*} \\[1em] \Rightarrow \begin{bmatrix*}[r] 4 & x \\ 0 & 4 \end{bmatrix*} = \begin{bmatrix*}[r] 4 + 0 & 4 + 4 \\ 0 + 0 & 0 + 4 \end{bmatrix*} \\[1em] \Rightarrow \begin{bmatrix*}[r] 4 & x \\ 0 & 4 \end{bmatrix*} = \begin{bmatrix*}[r] 4 & 8 \\ 0 & 4 \end{bmatrix*} \\[1em] \Rightarrow x = 8.$

Hence, Option 3 is the correct option.

The median of the following observations arranged in ascending order is 64. Find the value of x :

27, 31, 46, 52, x, x + 4, 71, 79, 85, 90

1. 60

2. 61

3. 62

4. 66

Answer

No. of observations = 10, which is even.

Median = $\dfrac{n}{2}\text{th term} = \dfrac{10}{2}$ = 5th term.

Given,

Median = 64

∴ x + 4 = 64

⇒ x = 64 - 4 = 60.

Hence, Option 1 is the correct option.

Points A(x, y), B(3, -2) and C(4, -5) are collinear. The value of y in terms of x is ∶

1. 3x - 11

2. 11 - 3x

3. 3x - 7

4. 7 - 3x

Answer

Since, points A, B and C are collinear.

∴ Slope of AB = Slope of BC.

$\Rightarrow \dfrac{-2 - y}{3 - x} = \dfrac{-5 - (-2)}{4 - 3} \\[1em] \Rightarrow \dfrac{-2 - y}{3 - x} = \dfrac{-5 + 2}{1} \\[1em] \Rightarrow \dfrac{-2 - y}{3 - x} = -3 \\[1em] \Rightarrow -2 - y = -3(3 - x) \\[1em] \Rightarrow -2 - y = -9 + 3x \\[1em] \Rightarrow y = -2 + 9 - 3x \\[1em] \Rightarrow y = 7 - 3x.$

Hence, Option 4 is the correct option.

The given table shows the distance covered and the time taken by a train moving at a uniform speed along a straight track.

The values of x and y are :

1. x = 4, y = 150

2. x = 3, y = 100

3. x = 4, y = 100

4. x = 3, y = 150

Answer

Speed = $\dfrac{\text{Distance}}{\text{Time}}$

Average speed = $\dfrac{60}{2}$ = 30 km/hr

$\Rightarrow \dfrac{90}{x} = 30 \\[1em] \Rightarrow x = \dfrac{90}{30} = 3. \\[1em] \phantom{\Rightarrow} \dfrac{y}{5} = 30 \\[1em] \Rightarrow y = 30 \times 5 = 150.$

Hence, Option 4 is the correct option.

The 7th term of the given Arithmetic Progression (A.P.):

$\dfrac{1}{a}, \Big(\dfrac{1}{a} + 1\Big), \Big(\dfrac{1}{a} + 2\Big), ......$ is :

1. $\Big(\dfrac{1}{a} + 6\Big)$

2. $\Big(\dfrac{1}{a} + 7\Big)$

3. $\Big(\dfrac{1}{a} + 8\Big)$

4. $\Big(\dfrac{1}{a} + 7^7\Big)$

Answer

In the A.P. :

$\dfrac{1}{a}, \Big(\dfrac{1}{a} + 1\Big), \Big(\dfrac{1}{a} + 2\Big), ......$

First term (x) = $\dfrac{1}{a}$

Common difference (d) = $\dfrac{1}{a} + 1 - \dfrac{1}{a}$ = 1.

x₇ = x + (7 - 1)d

= $\dfrac{1}{a} + 6 \times 1$

= $\Big(\dfrac{1}{a} + 6\Big)$.

Hence, Option 1 is the correct option.

The sum invested to purchase 15 shares of a company of nominal value ₹ 75 available at a discount of 20% is:

1. ₹ 60

2. ₹ 90

3. ₹ 1350

4. ₹ 900

Answer

N.V. = ₹ 75

Discount = 20%

M.V. = ₹ 75 - $\dfrac{20}{100} \times 75$

= ₹ 75 - ₹ 15

= ₹ 60.

Cost of 15 shares = 15 × ₹ 60 = ₹ 900.

Hence, Option 4 is the correct option.

The circumcentre of a triangle is the point which is ∶

1. at equal distance from the three sides of the triangle.

2. at equal distance from the three vertices of the triangle.

3. the point of intersection of the three medians.

4. the point of intersection of the three altitudes of the triangle.

Answer

The circumcenter of a triangle is defined as the point equidistant from the three vertices of the triangle.

Hence, Option 2 is the correct option.

Statement (i) : sin² θ + cos² θ = 1

Statement (ii) : cosec² θ + cot² θ = 1

Which of the following is valid ?

1. only (i)

2. only (ii)

3. both (i) and (ii)

4. neither (i) nor (ii)

Answer

Trigonometry identity :

sin² θ + cos² θ = 1

cosec² θ - cot² θ = 1

∴ Only statement (i) is correct.

Hence, Option 1 is the correct option.

In the given diagram, PS and PT are the tangents to the circle. SQ || PT and ∠SPT = 80°. The value of ∠QST is :

1. 140°

2. 90°

3. 80°

4. 50°

Answer

In △ PST,

⇒ PS = PT (Tangents from an external point to a circle are equal in length)

⇒ ∠PST = ∠PTS = a (let) (Angles opposite to equal sides are equal)

By angle sum property of triangle,

⇒ ∠PST + ∠PTS + ∠SPT = 180°

⇒ a + a + 80° = 180°

⇒ 2a = 180° - 80°

⇒ 2a = 100°

⇒ a = $\dfrac{100°}{2}$ = 50°.

From figure,

⇒ ∠QST = ∠STP = 50° (Alternate angles are equal)

Hence, Option 4 is the correct option.

Assertion (A): A die is thrown once and the probability of getting an even number is $\dfrac{2}{3}$.

Reason (R): The sample space for even numbers on a die is {2, 4, 6}

1. A is true, R is false.

2. A is false, R is true.

3. Both A and R are true.

4. Both A and R are false.

Answer

Sample space when a die is thrown = {1, 2, 3, 4, 5, 6}.

Sample space for even numbers = {2, 4, 6}

Probability of getting an even number = $\dfrac{3}{6} = \dfrac{1}{2}$.

∴ A is false and R is true.

Hence, Option 2 is the correct option.

A rectangular sheet of paper of size 11 cm x 7 cm is first rotated about the side 11 cm and then about the side 7 cm to form a cylinder, as shown in the diagram. The ratio of their curved surface areas is:

1. 1 : 1

2. 7 : 11

3. 11 : 7

4. $\dfrac{11π}{7} : \dfrac{7π}{11}$

Answer

In first case :

Height of cylinder (h) = 7 cm

Let radius be r cm

⇒ 2πr = 11

⇒ r = $\dfrac{11}{2π}$

In second case :

Height of cylinder (H) = 11 cm

Let radius be R cm

⇒ 2πR = 7

⇒ R = $\dfrac{7}{2π}$

$\therefore \dfrac{\text{CSA of 1st cylinder}}{\text{CSA of 2nd cylinder}} = \dfrac{2πrh}{2πRH} \\[1em] = \dfrac{rh}{RH} \\[1em] = \dfrac{\dfrac{11}{2π} \times 7}{\dfrac{7}{2π} \times 11} \\[1em] = \dfrac{\dfrac{77}{2π}}{\dfrac{77}{2π}} \\[1em] = \dfrac{1}{1} \\[1em] = 1 : 1.$

Hence, Option 1 is the correct option.

In the given diagram, ∆ABC ∼ ∆PQR. If AD and PS are bisectors of ∠BAC and ∠QPR respectively then:

1. ∆ABC ∼ ∆PQS

2. ∆ABD ∼ ∆PQS

3. ∆ABD ∼ ∆PSR

4. ∆ABC ∼ ∆PSR

Answer

Given,

∆ABC ∼ ∆PQR

∴ ∠A = ∠P

⇒ $\dfrac{∠A}{2} = \dfrac{∠P}{2}$

⇒ ∠BAD = ∠QPS

∠B = ∠Q [∵ ∆ABC ∼ ∆PQR]

In ∆ABD ∼ ∆PQS,

⇒ ∠BAD = ∠QPS

⇒ ∠B = ∠Q

∴ ∆ABD ∼ ∆PQS (By A.A. axiom)

Hence, Option 2 is the correct option.

A = $\begin{bmatrix*}[r] x & 0 \\ 1 & 1 \end{bmatrix*}, B = \begin{bmatrix*}[r] 4 & 0 \\ y & 1 \end{bmatrix*}\text{ and } C = \begin{bmatrix*}[r] 4 & 0 \\ x & 1 \end{bmatrix*}$.

Find the values of x and y, if AB = C.

Answer

$\phantom{\Rightarrow} AB = C \\[1em] \Rightarrow \begin{bmatrix*}[r] x & 0 \\ 1 & 1 \end{bmatrix*}\begin{bmatrix*}[r] 4 & 0 \\ y & 1 \end{bmatrix*} = \begin{bmatrix*}[r] 4 & 0 \\ x & 1 \end{bmatrix*} \\[1em] \Rightarrow \begin{bmatrix*}[r] x \times 4 + 0 \times y & x \times 0 + 0 \times 1 \\ 1 \times 4 + 1 \times y & 1 \times 0 + 1 \times 1 \end{bmatrix*} = \begin{bmatrix*}[r] 4 & 0 \\ x & 1 \end{bmatrix*} \\[1em] \Rightarrow \begin{bmatrix*}[r] 4x + 0 & 0 + 0 \\ 4 + y & 0 + 1 \end{bmatrix*} = \begin{bmatrix*}[r] 4 & 0 \\ x & 1 \end{bmatrix*} \\[1em] \Rightarrow \begin{bmatrix*}[r] 4x & 0 \\ 4 + y & 1 \end{bmatrix*} = \begin{bmatrix*}[r] 4 & 0 \\ x & 1 \end{bmatrix*} \\[1em] \Rightarrow 4x = 4 \text{ and } 4 + y = x \\[1em] \Rightarrow x = \dfrac{4}{4} \text{ and } 4 + y = x \\[1em] \Rightarrow x = 1 \text{ and } 4 + y = 1 \\[1em] \Rightarrow x = 1 \text{ and } y = 1 - 4 = -3.$

Hence, x = 1 and y = -3.

A solid metallic cylinder is cut into two identical halves along its height. The diameter of the cylinder is 7 cm and the height is 10 cm. Find :

(a) The total surface area (both the halves).

(b) The total cost of painting the two halves at the rate of ₹ 30 per cm².

$\Big(\text{use } \pi = \dfrac{22}{7}\Big)$

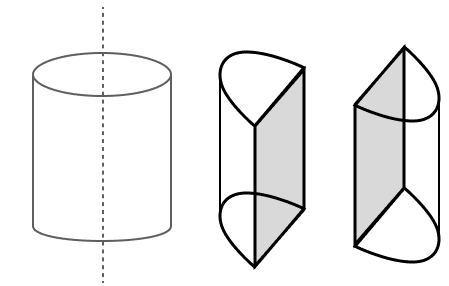
Answer

(a) Given,

Diameter of cylinder (d) = 7 cm

Radius of cylinder (r) = $\dfrac{d}{2} = \dfrac{7}{2}$ = 3.5 cm

Height of cylinder (h) = 10 cm

Total surface area (both the halves) = Total surface area of cylinder + Area of two rectangles

= [2πr(h + r)] + [2 × (l × b)]

= [2πr(h + r)] + [2 × (h × d)]

= $\Big[2 \times \dfrac{22}{7} \times 3.5 \times (3.5 + 10) \Big] + [2 \times 10 \times 7]$

= (2 × 22 × 0.5 × 13.5) + 140

= 297 + 140

= 437 cm².

Hence, total surface area of both the halves = 437 cm².

(b) Total cost of painting the two halves = Total surface area × Rate

= 437 × 30

= ₹ 13,110.

Hence, total cost of painting the two halves = ₹ 13,110.

15, 30, 60, 120 ...... are in G.P. (Geometric Progression).

(a) Find the nth term of this G.P. in terms of n.

(b) How many terms of the above G.P. will give the sum 945 ?

Answer

Given,

G.P. : 15, 30, 60, 120 ......

First term (a) = 15

Common ratio (r) = $\dfrac{30}{15}$ = 2

(a) nth term of G.P. = arⁿ = 15 x 2ⁿ

Hence, nth term of the given G.P. is 15 x 2ⁿ

(b) Let sum of n terms of G.P. is 945.

By formula,

Sum of n terms of G.P. = $\dfrac{a(r^n - 1)}{(r - 1)}$

Substituting values we get :

$\Rightarrow 945 = \dfrac{15.(2^n - 1)}{2 - 1} \\[1em] \Rightarrow 945 = \dfrac{15.(2^n - 1)}{1} \\[1em] \Rightarrow 2^n - 1 = \dfrac{945}{15} \\[1em] \Rightarrow 2^n - 1 = 63 \\[1em] \Rightarrow 2^n = 63 + 1 \\[1em] \Rightarrow 2^n = 64 \\[1em] \Rightarrow 2^n = 2^6 \\[1em] \Rightarrow n = 6.$

Hence, sum of 6 terms of G.P. = 945.

Factorize: sin³ θ + cos³ θ

Hence, prove the following identity :

$\dfrac{\text{sin}^3 θ + \text{cos}^3 θ}{\text{sin θ + cos θ}}$ + sin θ cos θ = 1

Answer

Factorizing,

⇒ sin³ θ + cos³ θ = (sin θ + cos θ)(sin² θ + cos² θ - sin θ cos θ)

⇒ sin³ θ + cos³ θ = (sin θ + cos θ)(1 - sin θ cos θ) ...........(1)

To prove,

$\dfrac{\text{sin}^3 θ + \text{cos}^3 θ}{\text{sin θ + cos θ}}$ + sin θ cos θ = 1

Substituting value of sin³ θ + cos³ θ from equation (1) in L.H.S. of above equation :

⇒ $\dfrac{\text{(sin θ + cos θ)(1 - sin θ cos θ)}}{\text{sin θ + cos θ}} + \text{sin θ cos θ}$

⇒ 1 - sin θ cos θ + sin θ cos θ

⇒ 1.

Since, L.H.S. = R.H.S.

Hence, proved that $\dfrac{\text{sin}^3 θ + \text{cos}^3 θ}{\text{sin θ + cos θ}} + \text{sin θ cos θ} = 1$.

In the given diagram, O is the centre of the circle. PR and PT are two tangents drawn from the external point P and touching the circle at Q and S respectively. MN is a diameter of the circle. Given ∠PQM = 42° and ∠PSM = 25°.

Find :

(a) ∠OQM

(b) ∠QNS

(c) ∠QOS

(d) ∠QMS

Answer

(a) From figure,

⇒ ∠OQP = 90° (Tangent is perpendicular to radius at the point of contact)

⇒ ∠OQM = ∠OQP - ∠PQM

⇒ ∠OQM = 90° - 42° = 48°.

Hence, ∠OQM = 48°.

(b) From figure,

⇒ ∠QNM = ∠PQM = 42° (By alternate segment theorem)

⇒ ∠SNM = ∠PSM = 25° (By alternate segment theorem)

⇒ ∠QNS = ∠QNM + ∠SNM

⇒ ∠QNS = 42° + 25° = 67°.

Hence, ∠QNS = 67°.

(c) We know that,

Angle subtended by an arc at the center is twice the angle subtended by the arc at any other point of the circle.

⇒ ∠QOS = 2∠QNS

⇒ ∠QOS = 2 × 67° = 134°.

Hence, ∠QOS = 134°.

(d) From figure,

QMSN is a cyclic quadrilateral.

We know that,

Sum of opposite angles of a cyclic quadrilateral is 180°.

⇒ ∠QMS + ∠QNS = 180°

⇒ ∠QMS + 67° = 180°

⇒ ∠QMS = 180° - 67° = 113°.

Hence, ∠QMS = 113°.

Use graph sheet for this question.

(a) Plot A(0, 3), B(2, 1) and C(4, -1).

(b) Reflect point B and C in y-axis and name their images as B' and C' respectively. Plot and write coordinates of the points B' and C'.

(c) Reflect point A in the line BB' and name its images as A'.

(d) Plot and write coordinates of point A'.

(e) Join the points ABA'B' and give the geometrical name of the closed figure so formed.

Answer

From figure,

Coordinates of point A' = (0, -1), B' = (-2, 1) and C' = (-4, -1).

The closed figure ABA'B' is a square.

Suresh has a recurring deposit account in a bank. He deposits ₹2000 per month and the bank pays interest at the rate of 8% per annum. If he gets ₹1040 as interest at the time of maturity, find in years total time for which the account was held.

Answer

Let time be n months.

By formula,

I = $P \times \dfrac{n(n + 1)}{2\times 12} \times \dfrac{r}{100}$

Substituting values we get :

$\Rightarrow 1040 = 2000 \times \dfrac{n(n + 1)}{24} \times \dfrac{8}{100} \\[1em] \Rightarrow 1040 = 2000 \times \dfrac{n(n + 1)}{300} \\[1em] \Rightarrow n(n + 1) = \dfrac{1040 \times 300}{2000} \\[1em] \Rightarrow n(n + 1) = 156 \\[1em] \Rightarrow n^2 + n - 156 = 0 \\[1em] \Rightarrow n^2 + 13n - 12n - 156 = 0 \\[1em] \Rightarrow n(n + 13) - 12(n + 13) = 0 \\[1em] \Rightarrow (n - 12)(n + 13) = 0 \\[1em] \Rightarrow n - 12 = 0 \text{ or } n + 13 = 0 \\[1em] \Rightarrow n = 12 \text{ or } n = -13.$

Since, no. of months cannot be negative.

∴ n = 12.

Hence, total time for which the account was held = 12 months.

The following table gives the duration of movies in minutes.

Using step–deviation method, find the mean duration of the movies.

Answer

In the given table i is the class interval which is equal to 10.

Mean = A + $\dfrac{Σfu}{Σf} \times i = 135 + \dfrac{-38}{50} \times 10$

= $135 + \dfrac{-380}{50}$

= 135 - 7.6

= 127.4

Hence, mean = 127.4

If $\dfrac{(a + b)^3}{(a - b)^3} = \dfrac{64}{27}$

(a) Find $\dfrac{a + b}{a - b}$

(b) Hence using properties of proportion, find a : b.

Answer

(a) Solving,

$\Rightarrow \dfrac{(a + b)^3}{(a - b)^3} = \dfrac{64}{27} \\[1em] \Rightarrow \dfrac{(a + b)^3}{(a - b)^3} = \dfrac{4^3}{3^3} \\[1em] \Rightarrow \Big(\dfrac{a + b}{a - b}\Big)^3 = \Big(\dfrac{4}{3}\Big)^3 \\[1em] \Rightarrow \dfrac{a + b}{a - b} = \dfrac{4}{3} \\[1em]$

Hence, $\dfrac{a + b}{a - b} = \dfrac{4}{3}.$

(b) Solving further,

$\Rightarrow 3(a + b) = 4(a - b) \\[1em] \Rightarrow 3a + 3b = 4a - 4b \\[1em] \Rightarrow 4a - 3a = 3b + 4b \\[1em] \Rightarrow a = 7b \\[1em] \Rightarrow \dfrac{a}{b} = \dfrac{7}{1} \\[1em] \Rightarrow a : b = 7 : 1.$

Hence, a : b = 7 : 1.

The given graph with a histogram represents the number of plants of different heights grown in a school campus. Study the graph carefully and answer the following questions :

(a) Make a frequency table with respect to the class boundaries and their corresponding frequencies.

(b) State the modal class.

(c) Identify and note down the mode of the distribution.

(d) Find the number of plants whose height range is between 80 cm to 90 cm.

Answer

(a) Frequency table :

(b) From graph,

The modal class is 60-70.

(c) From graph,

The mode = 64.

(d) From graph,

The number of plants whose height range is between 80 cm to 90 cm are 3.

The angle of elevation of the top of a 100 m high tree from two points A and B on the opposite side of the tree are 52° and 45° respectively. Find the distance AB, to the nearest metre.

Answer

From figure,

⇒ tan 52° = $\dfrac{CD}{AC}$

⇒ 1.28 = $\dfrac{100}{AC}$

⇒ AC = $\dfrac{100}{1.28}$ = 78.125 m

⇒ tan 45° = $\dfrac{CD}{BC}$

⇒ 1 = $\dfrac{100}{BC}$

⇒ BC = 100 m

⇒ AB = AC + BC = 78.125 + 100 = 178.125 m

Hence, AB = 178.125 m

Solve the following quadratic equation for x and give your answer correct to three significant figures :

2x² - 10x + 5 = 0

Answer

Comparing equation 2x² - 10x + 5 = 0 with ax² + bx + c = 0, we get :

a = 2, b = -10 and c = 5

By formula,

⇒ x = $\dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

Substituting values we get :

$\Rightarrow x = \dfrac{-(-10) \pm \sqrt{(-10)^2 - 4 \times 2 \times 5}}{2 \times 2} \\[1em] = \dfrac{10 \pm \sqrt{100 - 40}}{4} \\[1em] = \dfrac{10 \pm \sqrt{60}}{4} \\[1em] = \dfrac{10 \pm 2\sqrt{15}}{4} \\[1em] = \dfrac{2(5 \pm \sqrt{15})}{4} \\[1em] = \dfrac{5 \pm \sqrt{15}}{2} \\[1em] = \dfrac{5 \pm 3.87}{2} \\[1em] = \dfrac{5 + 3.87}{2}, \dfrac{5 - 3.87}{2} \\[1em] = \dfrac{8.87}{2}, \dfrac{1.13}{2} \\[1em] = 4.44, 0.565$

Hence, x = 4.44, 0.565

The n^th term of an Arithmetic Progression (A.P.) is given by the relation T_n = 6(7 - n). Find ∶

(a) its first term and common difference

(b) sum of its first 25 terms

Answer

(a) T_n = 6(7 - n)

Substituting n = 1, we get :

T₁ = 6(7 - 1) = 6 × 6 = 36.

Substituting n = 2, we get :

T₂ = 6(7 - 2) = 6 × 5 = 30.

Common difference (d) = T₂ - T₁

= 30 - 36 = -6.

Hence, common difference (d) = -6 and first term = 36.

(b) By formula,

Sum upto n terms = $\dfrac{n}{2}[2a + (n - 1)d]$

$\text{Sum upto 25 terms} = \dfrac{25}{2}[2 \times 36 + (25 - 1) \times -6] \\[1em] = 12.5 \times [72 + 24 \times -6] \\[1em] = 12.5 \times [72 - 144] \\[1em] = 12.5 \times -72 \\[1em] = -900.$

Hence, sum of its first 25 terms = -900.

In the given diagram ∆ADB and ∆ACB are two right angled triangles with ∠ADB = ∠BCA = 90°. If AB = 10 cm, AD = 6 cm, BC = 2.4 cm and DP = 4.5 cm

(a) Prove that ∆APD ∼ ∆BPC.

(b) Find the length of BD and PB

(c) Hence, find the length of PA

(d) Find area ∆APD : area ∆BPC

Answer

(a) In ∆APD and ∆BPC,

⇒ ∠APD = ∠BPC (Vertically opposite angles are equal)

⇒ ∠ADP = ∠BCP (Both equal to 90°)

Hence, proved that ∆APD ∼ ∆BPC.

(b) In ∆ADB,

By pythagoras theorem,

⇒ AB² = AD² + BD²

⇒ 10² = 6² + BD²

⇒ BD² = 100 - 36

⇒ BD² = 64

⇒ BD = $\sqrt{64}$ = 8 cm.

⇒ PB = BD - PD = 8 - 4.5 = 3.5 cm

Hence, BD = 8 cm and PB = 3.5 cm.

(c) In ∆APD,

By pythagoras theorem,

⇒ AP² = AD² + DP²

⇒ AP² = 6² + (4.5)²

⇒ AP² = 36 + 20.25

⇒ AP² = 56.25

⇒ AP = $\sqrt{56.25}$ = 7.5 cm

Hence, length of AP = 7.5 cm.

(d) We know that,

Ratio of area of similar triangles is equal to the square of the corresponding sides.

$\therefore \dfrac{\text{Area of △APD}}{\text{Area of △BPC}} = \dfrac{AD^2}{BC^2} \\[1em] = \dfrac{6^2}{(2.4)^2} \\[1em] = \dfrac{6 \times 6}{2.4 \times 2.4} \\[1em] = \dfrac{1 \times 1}{0.4 \times 0.4} \\[1em] = \dfrac{10 \times 10}{4 \times 4} \\[1em] = \dfrac{100}{16} \\[1em] = \dfrac{25}{4} \\[1em] = 25 : 4.$

Hence, area ∆APD : area ∆BPC = 25 : 4.

In the given diagram, an isosceles ∆ABC is inscribed in a circle with centre O. PQ is a tangent to the circle at C. OM is perpendicular to chord AC and ∠COM = 65°. Find :

(a) ∠ABC

(b) ∠BAC

(c) ∠BCQ

Answer

(a) From figure,

∠AOC = ∠AOM + ∠COM = 65° + 65° = 130°.

We know that,

Angle at the center is twice the angle formed by the same arc at any other point of the circle.

⇒ ∠AOC = 2∠ABC

⇒ ∠ABC = $\dfrac{1}{2} \times ∠AOC = \dfrac{1}{2} \times 130°$ = 65°.

Hence, ∠ABC = 65°.

(b) In △ABC,

⇒ AB = AC (Given)

⇒ ∠ACB = ∠ABC = 65° (Opposite angles of equal sides are equal)

By angle sum property of triangle,

⇒ ∠ACB + ∠ABC + ∠BAC = 180°

⇒ 65° + 65° + ∠BAC = 180°

⇒ ∠BAC = 180° - 65° - 65° = 50°.

Hence, ∠BAC = 50°.

(c) We know that,

The angle formed between the tangent and the chord through the point of contact of the tangent is equal to the angle formed by the chord in the alternate segment.

∴ ∠BCQ = ∠BAC = 50°.

Hence, ∠BCQ = 50°.

Solve the following inequation, write down the solution set and represent it on the real number line.

-3 + x ≤ $\dfrac{7x}{2} + 2$ < 8 + 2x, x ∈ I.

Answer

Given,

-3 + x ≤ $\dfrac{7x}{2} + 2$ < 8 + 2x

Solving L.H.S. of the above inequation :

$\Rightarrow -3 + x \le \dfrac{7x}{2} + 2 \\[1em] \Rightarrow \dfrac{7x}{2} -x \ge -3 - 2 \\[1em] \Rightarrow \dfrac{7x - 2x}{2} \ge -5 \\[1em] \Rightarrow \dfrac{5x}{2} \ge -5 \\[1em] \Rightarrow x \ge \dfrac{-5 \times 2}{5} \\[1em] \Rightarrow x \ge -2 \text{ ..........(1)}$

Solving R.H.S. of the above inequation :

$\Rightarrow \dfrac{7x}{2} + 2 \lt 8 + 2x \\[1em] \Rightarrow \dfrac{7x}{2} - 2x \lt 8 - 2 \\[1em] \Rightarrow \dfrac{7x - 4x}{2} \lt 6 \\[1em] \Rightarrow \dfrac{3x}{2} \lt 6 \\[1em] \Rightarrow x \lt \dfrac{6 \times 2}{3} \\[1em] \Rightarrow x \lt 4 \text{ ..........(2)}$

From inequation (1) and (2), we get :

-2 ≤ x < 4.

Since, x ∈ I.

x = {-2, -1, 0, 1, 2, 3}.

Hence, solution set = {-2, -1, 0, 1, 2, 3}.

In the given diagram, ABC is a triangle, where B(4, -4) and C(-4, -2). D is a point on AC.

(a) Write down the coordinates of A and D.

(b) Find the coordinates of the centroid of ∆ABC.

(c) If D divides AC in the ratio k : 1, find the value of k.

(d) Find the equation of the line BD.

Answer

(a) From graph,

Co-ordinates of A = (0, 6) and D = (-3, 0)

(b) By formula,

Co-ordinates of centroid = $\Big(\dfrac{x_1 + x_2 + x_3}{3}, \dfrac{y_1 + y_2 + y_3}{3}\Big)$

$= \Big(\dfrac{0 + 4 + (-4)}{3}, \dfrac{6 + (-4) + (-2)}{3}\Big) \\[1em] = \Big(\dfrac{0}{3}, \dfrac{0}{3}\Big) \\[1em] = (0, 0).$

Hence, co-ordinates of centroid of ∆ABC = (0, 0).

(c) By section-formula,

(x, y) = $\Big(\dfrac{m_1x_2 + m_2x_1}{m_1 + m_2}, \dfrac{m_1y_2 + m_2y_1}{m_1 + m_2}\Big)$

Given,

D divides AC in the ratio k : 1.

$\therefore (-3, 0) = \Big(\dfrac{k \times -4 + 1 \times 0}{k + 1}, \dfrac{k \times -2 + 1 \times 6}{k + 1}\Big) \\[1em] \Rightarrow (-3, 0) = \Big(\dfrac{-4k + 0}{k + 1}, \dfrac{-2k + 6}{k + 1}\Big) \\[1em] \Rightarrow (-3, 0) = \Big(\dfrac{-4k}{k + 1}, \dfrac{-2k + 6}{k + 1}\Big) \\[1em] \Rightarrow -3 = -\dfrac{4k}{k + 1} \text{ and } 0 = \dfrac{-2k + 6}{k + 1} \\[1em] \Rightarrow -3(k + 1) = -4k \text{ and } 0 = -2k + 6 \\[1em] \Rightarrow 3(k + 1) = 4k \text{ and } 2k = 6 \\[1em] \Rightarrow 3k + 3 = 4k \text{ and } k = \dfrac{6}{2} \\[1em] \Rightarrow 4k - 3k = 3 \text{ and } k = 3 \\[1em] \Rightarrow k = 3.$

Hence, k = 3.

(d) By two point form,

Equation of line :

y - y₁ = $\dfrac{y_2 - y_1}{x_2 - x_1}(x - x_1)$

Equation of BD :

⇒ y - (-4) = $\dfrac{0 - (-4)}{-3 - 4}(x - 4)$

⇒ y + 4 = $\dfrac{4}{-7}(x - 4)$

⇒ -7(y + 4) = 4(x - 4)

⇒ -7y - 28 = 4x - 16

⇒ 4x + 7y - 16 + 28 = 0

⇒ 4x + 7y + 12 = 0.

Hence, equation of BD is 4x + 7y + 12 = 0.

The polynomial 3x³ + 8x² - 15x + k has (x - 1) as a factor. Find the value of k. Hence factorize the resulting polynomial completely.

Answer

⇒ x - 1 = 0

⇒ x = 1.

Given, (x - 1) is a factor of 3x³ + 8x² - 15x + k.

Thus, on substituting x = 1 in 3x³ + 8x² - 15x + k, the remainder will be zero.

⇒ 3.(1)³ + 8.(1)² - 15(1) + k = 0

⇒ 3.1 + 8.1 - 15 + k = 0

⇒ 3 + 8 - 15 + k = 0

⇒ 11 - 15 + k = 0

⇒ k - 4 = 0

⇒ k = 4.

Polynomial = 3x³ + 8x² - 15x + 4

On dividing (3x³ + 8x² - 15x + 4) by (x - 1), we get :

$\begin{array}{l} \phantom{x - 1)}{\quad 3x^2 + 11x - 4} \\ x - 1\overline{\smash{\big)}\quad 3x^3 + 8x^2 - 15x + 4} \\ \phantom{x - 1)}\phantom{)}\underline{\underset{-}{+}3x^3 \underset{+}{-}3x^2} \\ \phantom{{x - 1}31x^3-2}11x^2 - 15x \\ \phantom{{x - 1)}x^3-2}\underline{\underset{-}{+}11x^2 \underset{+}{-} 11x} \\ \phantom{{x - 1)}31x^3-2+1}-4x + 4 \\ \phantom{{x - 1)}31x^3-2+11}\underline{\underset{+}{-}4x \underset{-}{+} 4} \\ \phantom{{x - 1)}31x^3-2+11+1}\times \end{array}$

⇒ 3x³ + 8x² - 15x + 4 = (x - 1)(3x² + 11x - 4)

= (x - 1)[3x² + 12x - x - 4]

= (x - 1)[3x(x + 4) - 1(x + 4)]

= (x - 1)(3x - 1)(x + 4).

Hence, 3x³ + 8x² - 15x + 4 = (x - 1)(3x - 1)(x + 4).

The following letters A, D, M, N, O, S, U, Y of the English alphabet are written on separate cards and put in a box. The cards are well shuffled and one card is drawn at random. What is the probability that the card drawn is a letter of the word,

(a) MONDAY?

(b) which does not appear in MONDAY?

(c) which appears both in SUNDAY and MONDAY?

Answer

Letters written on cards = {'A', 'D', 'M', 'N', 'O', 'S', 'U', 'Y'}

No. of cards = 8

(a) Letters of the word MONDAY present in the cards = {'M', 'O', 'N', 'D', 'A', 'Y'}

Probability that the card drawn is a letter of the word MONDAY

= $\dfrac{\text{Letters of MONDAY present}}{\text{No. of cards}} = \dfrac{6}{8} = \dfrac{3}{4}$.

Hence, required probability = $\dfrac{3}{4}$.

(b) Letters of the word not present in MONDAY = {'S', 'U'}

Probability that the card drawn is not a letter of the word MONDAY

= $\dfrac{\text{Letters not present in MONDAY}}{\text{No. of cards}} = \dfrac{2}{8} = \dfrac{1}{4}$.

Hence, required probability = $\dfrac{1}{4}$.

(c) Letters of the word present in SUNDAY and MONDAY are {'N', 'D', 'A', 'Y'}.

Probability that the card drawn has a letter which appears both in SUNDAY and MONDAY

= $\dfrac{\text{Letters present in both MONDAY and SUNDAY}}{\text{No. of cards}} = \dfrac{4}{8} = \dfrac{1}{2}$.

Hence, required probability = $\dfrac{1}{2}$.

Oil is stored in a spherical vessel occupying $\dfrac{3}{4}$ of its full capacity. Radius of this spherical vessel is 28 cm. This oil is then poured into a cylindrical vessel with a radius of 21 cm. Find the height of the oil in the cylindrical vessel (correct to the nearest cm).

Take $\pi = \dfrac{22}{7}$

Answer

Given,

Radius of spherical vessel (r) = 28 cm

Volume of spherical vessel (v) = $\dfrac{4}{3}πr^3$

Volume of oil in vessel = $\dfrac{3}{4}v$

Substituting values we get :

$\Rightarrow v = \dfrac{4}{3} \times \dfrac{22}{7} \times 28^3 \\[1em] \Rightarrow \dfrac{3}{4}v = \dfrac{3}{4} \times \dfrac{4}{3} \times \dfrac{22}{7} \times 28^3 \\[1em] \Rightarrow \dfrac{3}{4}v = \dfrac{22}{7} \times 28^3.$

Radius of cylindrical vessel (R) = 21 cm

Let height of oil in cylindrical vessel be h cm.

Volume of oil = Volume of cylinder upto which oil is filled (πR²h)

$\Rightarrow \dfrac{22}{7} \times 28^3 = \dfrac{22}{7} \times 21^2 \times h \\[1em] \Rightarrow 28^3 = 21^2 \times h \\[1em] \Rightarrow h = \dfrac{28^3}{21^2}\\[1em] \Rightarrow h = \dfrac{21952}{441} \\[1em] \Rightarrow h = 49.77 ≈ 50 \text{ cm}.$

Hence, height of the oil in the cylindrical vessel = 50 cm.

The figure shows a circle of radius 9 cm with O as the centre. The diameter AB produced meets the tangent PQ at P. If PA = 24 cm, find the length of tangent PQ.

Answer

Given,

Radius of circle (r) = OA = OB = 9 cm

From figure,

AB = OA + OB = 9 + 9 = 18 cm

PB = PA - AB = 24 - 18 = 6 cm

We know that,

If a secant segment and tangent segment are drawn to a circle from the same external point, the length of the tangent segment is the geometric mean between the length of the secant segment and the length of the external part of the secant segment.

⇒ PQ² = PB × PA

⇒ PQ² = 6 × 24

⇒ PQ² = 144

⇒ PQ = $\sqrt{144}$ = 12 cm.

Hence, length of tangent PQ = 12 cm.

Mr. Gupta invested ₹33000 in buying ₹100 shares of a company at 10% premium. The dividend declared by the company is 12%.

Find:

(a) the number of shares purchased by him.

(b) his annual dividend.

Answer

Money invested = ₹33000

N.V. of share = ₹100

M.V. = N.V + Premium

= ₹100 + $\dfrac{10}{100} \times 100$

= ₹100 + ₹10

= ₹110.

(a) Number of shares = $\dfrac{\text{Money invested}}{\text{M.V.}} = \dfrac{33000}{110}$ = 300.

Hence, no. of shares purchased = 300.

(b) By formula,

Annual dividend = Number of shares × Rate of dividend × N.V.

= 300 × $\dfrac{12}{100} \times 100$

= ₹3600.

Hence, annual dividend = ₹3600.

A life insurance agent found the following data for distribution of ages of 100 policy holders:

On a graph sheet draw an ogive using the given data. Take 2 cm = 5 years along one axis and 2 cm = 10 policy holders along the other axis. Use your graph to find:

(a) The median age.

(b) Number of policy holders whose age is above 52 years.

Answer

Steps of construction :

1. Take 2 cm = 5 years on x-axis.

2. Take 1 cm = 10 policy holders on y-axis.

3. Plot the points (20, 0), (25, 2), (30, 6), (35, 18), (40, 38), (45, 66), (50, 88), (55, 96) and (60, 100).

4. Join the points by a free-hand curve.

Here, n = 100

Median = $\dfrac{n}{2} = \dfrac{100}{2}$ = 50th term

(a) Through J = 50 draw a horizontal line to meet the ogive at K. Through K, draw a vertical line to meet the x-axis at L. The abscissa of the point L represents 42.

Hence, the median age = 42 years.

(b) Through M = 52 draw a vertical line to meet the ogive at N. Through N, draw a horizontal line to meet the y-axis at O. The ordinate of the point O represents 91.

Hence, 91 people have their age less than or equal to 52.

∴ No. of people whose age is greater than 52 = 100 - 91 = 9.

Hence, number of policy holders whose age is above 52 years equal to 9.

Rohan bought the following eatables for his friends :

Soham Sweet Mart : Bill

Calculate :

(a) Total GST paid.

(b) Total bill amount including GST.

Answer

For Laddu :

Total cost = ₹ 500 × 2 = ₹ 1000

GST = $\dfrac{5}{100} \times 1000$ = ₹50

Total amount (including GST) = 1000 + 50 = ₹ 1050.

For pastries :

Total cost = ₹ 100 × 12 = ₹ 1200

GST = $\dfrac{18}{100} \times 1200$ = ₹ 216

Total amount (including GST) = 1200 + 216 = ₹ 1416.

(a) Total GST paid = ₹50 + ₹216 = ₹266.

Hence, total GST paid = ₹266.

(b) Total bill (including GST) = ₹ 1050 + ₹ 1416 = ₹ 2466.

Hence, total bill = ₹ 2466.

(a) If the lines kx - y + 4 = 0 and 2y = 6x + 7 are perpendicular to each other, find the value of k.

(b) Find the equation of a line parallel to 2y = 6x + 7 and passing through (-1, 1)

Answer

(a) 1st equation :

⇒ kx - y + 4 = 0

⇒ y = kx + 4

Slope (s₁) : k

2nd equation :

⇒ 2y = 6x + 7

⇒ y = $\dfrac{6}{2}x + \dfrac{7}{2}$

⇒ y = 3x + $\dfrac{7}{2}$

Slope (s₂) : 3

We know that,

Product of slope of perpendicular lines = -1

⇒ k × 3 = -1

⇒ k = $-\dfrac{1}{3}$

Hence, k = $-\dfrac{1}{3}$.

(b) We know that,

Slope of parallel lines are equal.

Slope of line parallel to line 2y = 6x + 7 is 3.

By point-slope form :

⇒ y - y₁ = m(x - x₁)

⇒ y - 1 = 3[x - (-1)]

⇒ y - 1 = 3[x + 1]

⇒ y - 1 = 3x + 3

⇒ y = 3x + 3 + 1

⇒ y = 3x + 4.

Hence, equation of line parallel to 2y = 6x + 7 and passing through (–1, 1) is y = 3x + 4.

Use ruler and compass to answer this question. Construct ∠ABC = 90°, where AB = 6 cm, BC = 8 cm.

(a) Construct the locus of points equidistant from B and C.

(b) Construct the locus of points equidistant from A and B.

(c) Mark the point which satisfies both the conditions (a) and (b) as O. Construct the locus of points keeping a fixed distance OA from the fixed point O.

(d) Construct the locus of points which are equidistant from BA and BC.

Answer

Steps of construction :

1. Draw a line segment BC = 8 cm

2. Construct ∠ABC = 90°, such that AB = 6 cm.

3. Draw XY, the perpendicular bisector of BC.

4. Draw PQ, the perpendicular bisector of AB.

5. Mark point O, the intersection of segment XY and PQ.

6. Draw BZ, the angle bisector of AB and BC.

We know that,

Locus of points equidistant from two points is the perpendicular bisector of the line joining the two points segment.

(a) Locus of points equidistant from B and C is XY.

(b) Locus of points equidistant from A and B is PQ.

We know that,

Locus of points equidistant from two sides is the angular bisector of angle between them.

(d) Locus of points which are equidistant from BA and BC is BZ.