Study of Gas Laws

Exercise 7 — Multiple Choice Type

Question 1

The graph of PV vs P for a gas is :

1. parabolic
2. hyperbolic
3. a straight line parallel to X-axis
4. a straight line passing through origin

Answer

a straight line parallel to X-axis

Reason — The graph of PV vs P is a straight line parallel to the pressure axis.

Question 2

The absolute temperature value that corresponds to 27°C is :

1. 200 K
2. 300 K
3. 400 K
4. 246 K

Answer

300 K

Reason — Celsius values can be converted to Kelvin values by adding 273 to degree celsius values. Hence, 27°C + 273 = 300 K

Question 3

Volume-temperature relationship is given by :

1. Boyle
2. Gay Lussac
3. Dalton
4. Charles

Answer

Charles

Reason — Charles' law states that volume of a given mass of a dry gas is directly proportional to its absolute (Kelvin) temperature, if the pressure remains constant.

Question 4

If pressure is doubled for a fixed mass of a gas, its volume will become :

1. 4 times
2. 1⁄2 times
3. 2 times
4. No change

Answer

1⁄2 times

Reason — According to Boyle's law volume of a given mass of a dry gas is inversely proportional to its pressure at constant temperature.

Hence, if pressure is doubled for a fixed mass of a gas, its volume will become 1⁄2 times.

Question 5

The S.I. unit of temperature is :

1. Pascal
2. °C
3. Kelvin
4. °F

Answer

Kelvin

Reason — The S.I. unit of temperature is Kelvin.

Question 6

Which of the following temperatures is known as the steam point ?

1. 273 K
2. 373 K
3. 290 K
4. 273°C

Answer

373 K

Reason — The steam point on Celsius scale is 100°C and corresponding to that steam point on Kelvin scale is 273 + 100 = 373 K.

Question 7

The graph shown below gives the statement for :

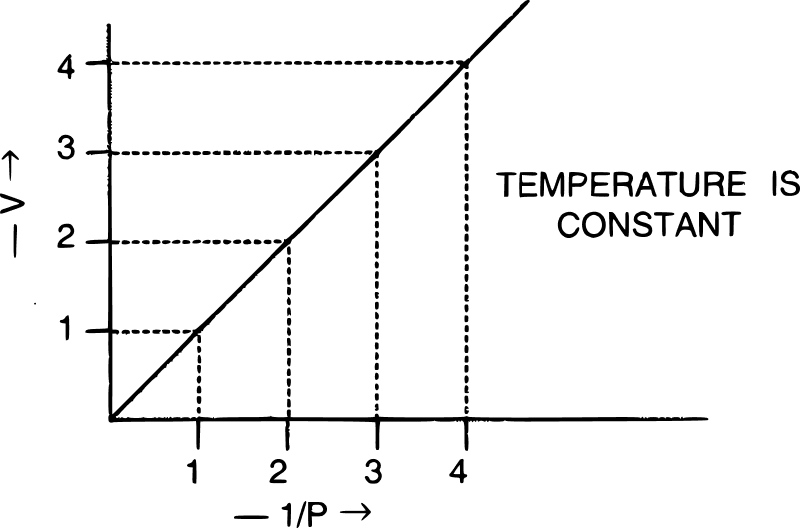
1. Henry's law
2. Charles' law
3. Boyle's law
4. Daltons' law

Answer

Boyle's law

Reason — For graphical verification of Boyle's law a graph of V vs 1/P is a straight line passing through the origin.

Question 8

'The volume of a given amount of a gas is directly proportional to its absolute temperature at a constant pressure' is the statement of :

1. Gay-Lussac's law
2. Boyle's law
3. Charles' law
4. Mendeleev's law

Answer

Charles' law

Reason — Charles' law states that volume of a given mass of a dry gas is directly proportional to its absolute (Kelvin) temperature, if the pressure remains constant.

Question 9

The volume of a given mass of a gas at constant temperature and 10 atmospheric pressure is 10 litres. Its volume at 5 atmospheres will be :

1. 5 litres
2. 10 litres
3. 15 litres
4. 20 litres

Answer

20 litres

Reason — Given,

V₁ = 10 l
P₁ = 10 atm
P₂ = 5 atm
V₂ = ?

According to Boyle's law, P₁V₁ = P₂V₂

So, 10 x 10 = 5 x V₂

V₂ = $\dfrac{100}{5}$ = 20 l

Question 10

STP is called standard temperature and pressure. The standard temperature and standard pressure respectively are :

1. 273 K and 760 mm
2. 0°C and 760 cm
3. 273°C and 1 atmosphere
4. 373 K and 76 cm

Answer

273 K and 760 mm

Reason — The standard values chosen are 0°C or 273 K for temperature and 1 atm or 760 mm of Hg for pressure. These values are known as standard temperature and pressure (STP).

Exercise 7 — Very Short Answer Type

Question 1

Match the following:

Answer

Question 2

Fill in the blanks:

(a) The average kinetic energy of the molecules of a gas is proportional to the ...............

(b) The temperature on the Kelvin scale at which molecular motion completely ceases is called ...............

(c) If the temperature is reduced to half, ............... would also reduce to half.

(d) The melting point of ice is ............... Kelvin.

Answer

(a) The average kinetic energy of the molecules of a gas is proportional to the absolute temperature.

(b) The temperature on the Kelvin scale at which molecular motion completely ceases is called absolute zero.

(c) If the temperature is reduced to half, volume would also reduce to half.

(d) The melting point of ice is 273 Kelvin.

Question 3

Correct the following statements, wherever necessary.

(a) The volume of a gas is inversely proportional to its pressure at constant temperature.

(b) Volume of a fixed mass of a gas is directly proportional to its temperature, pressure remaining constant.

(c) 0°C is equal to zero Kelvin.

(d) Standard temperature is 25°C.

(e) The boiling point of water is 273 K.

Answer

(a) The volume of a given mass of a dry gas is inversely proportional to its pressure at constant temperature.

(b) Volume of a fixed mass of a dry gas is directly proportional to its absolute temperature (Kelvin), pressure remaining constant.

(c) 0°C is equal to 273 Kelvin

(d) Standard temperature is 0°C or 273 K.

(e) The boiling point of water is 373 K.

Question 4

State (i) the three variables for gas laws (ii) S.I. units of these variables.

Answer

(i) The three variables for gas laws are Volume (V), Pressure (P), Temperature (T)

(ii) S.I. units of these variables:

Volume: Cubic metre (m³)

Pressure: Pascal (Pa)

Temperature: Kelvin (K)

Question 5

Write the value of:

(a) Standard temperature in:

(i) °C (ii) K

(b) Standard pressure in:

(i) atm (ii) mm Hg (iii) cm Hg (iv) torr

Answer

(a) Standard temperature

(i) 0°C (ii) 273 K

(b) Standard pressure

(i) 1 atmospheric pressure (atm)

(ii) 760 mm Hg

(iii) 76 cm of Hg

(iv) 760 torr

Question 6

State the following:

(a) Volume of a gas at 0 Kelvin.

(b) Absolute temperature of a gas at 7°C.

(c) Gas equation.

(d) Ice point in absolute temperature.

(e) S.T.P. conditions

Answer

(a) Volume of a gas at 0 Kelvin is zero.

(b) Absolute temperature of a gas at 7°C is 7 + 273 = 280 K.

(c) The gas equation is

$\dfrac{\text{P}_1\text{V}_1}{\text{T}_1}$ = $\dfrac{\text{P}_2\text{V}_2}{\text{T}_2}$

(d) Ice point in absolute temperature = 0 + 273 = 273 K

(e) Standard temperature = 0°C = 273 K
Standard pressure = 760 mm Hg = 76 cm Hg = 1 atmosphere (atm)

Exercise 7 — Short Answer Type

Question 1

What do you understand by gas?

Answer

Gas is a state of matter in which inter-particle attraction is weak and inter-particle space is so large that the particles become completely free to move randomly in the entire available space.

Question 2

What is diffusion ? Give an example to illustrate it.

Answer

Diffusion is the process of gradual mixing of two substances, kept in contact, by molecular motion.

If a jar of chlorine is opened in one end of the room, the odour of the gas can be detected in the entire room, because its particles start moving in a haphazard manner in all directions, till there is an equal concentration throughout the room.

Question 3

How is molecular motion related with temperature?

Answer

Molecular motion is directly proportional to temperature. When temperature increases molecular motion increases and when temperature decreases molecular motion decreases.

Question 4

Define absolute zero and absolute scale of temperature.

Answer

The temperature on the Kelvin scale at which molecular motion completely ceases is called absolute zero. Absolute zero is -273°C.

The temperature scale with its zero at -273.15°C and whose each degree is equal to one degree on the Celsius scale, is called the Kelvin or absolute scale of temperature.

Question 5

(a) Define S.T.P.

(b) Why is it necessary to compare gases at S.T.P.?

Answer

(a) The standard values chosen are 0°C or 273 K for temperature, and 1 atmospheric unit (atm) or 760 mm Hg for pressure. These standard values are known as standard temperature and pressure (S.T.P.).

(b) Since volume of a gas changes remarkably with change in temperature and pressure, it becomes necessary to choose standard values of temperature and pressure to which gas volumes can be referred.

Question 6

State the laws which are represented by the following graphs.

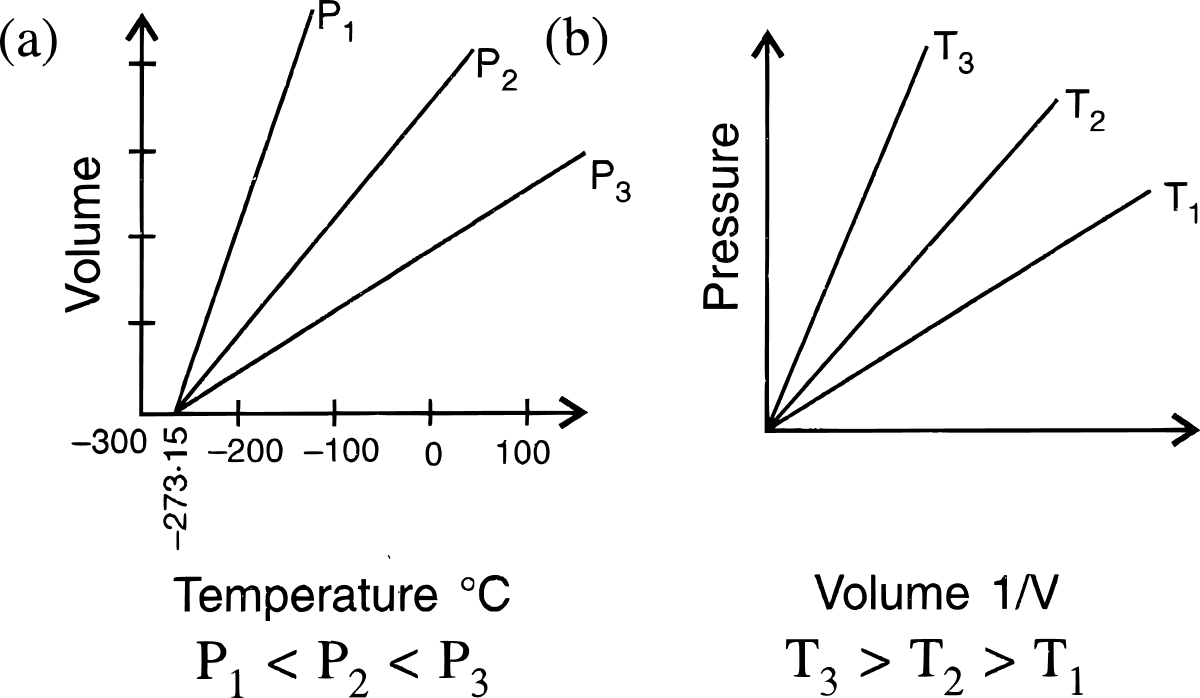
Answer

(a) Charles' law

(b) Boyle's law

Question 7

What is the relationship between the Celsius and the Kelvin scales of temperature?

Answer

The size of 1 degree on the Kelvin scale is the same as the size of 1 degree on the Celsius scale i.e., unit size on Kelvin scale is equal to the unit size on Celsius scale.
The value on the Celsius scale can be converted to Kelvin scale by adding 273 to it. Kelvin scale values can be converted to degree Celsius values by subtracting 273 from it.

Question 8

The molecular theory states that the pressure exerted by a gas in closed vessel results from the gas molecules striking against the walls of the vessel. How will the pressure change if :

(a) the temperature is doubled keeping the volume constant

(b) the volume is made half of its original value keeping the temperature constant?

Answer

(a) This can be explained on the basis of Gas equation

$\dfrac{\text{P}_1\text{V}_1}{\text{T}_1}$ = $\dfrac{\text{P}_2\text{V}_2}{\text{T}_2}$

When volume is constant we get,

$\dfrac{\text{P}_1}{\text{T}_1}$ = $\dfrac{\text{P}_2}{\text{T}_2}$

Hence, when temperature is doubled, pressure is doubled, as pressure and temperature are directly proportional.

(b) This can be explained on the basis of Boyle's law

P₁V₁ = P₂V₂

Hence, when the volume is made half of its original value keeping the temperature constant, pressure becomes double, as pressure and volume are inversely proportional.

Question 9

(a) What is the need for the Kelvin scale of temperature?

(b) What is the boiling point of water on the Kelvin scale? Convert it into centigrade scale.

Answer

(a) Kelvin scale makes application and use of gas laws simple. More significantly, all values on Kelvin scale are positive.

(b) Boiling point of water on the Kelvin scale is 373 K.

Temperature in °C = K - 273

So, 373 K - 273 = 100°C.

Question 10

Give reasons for the following :

(a) All temperatures in the absolute (Kelvin) scale are in positive figures.

(b) Gases have lower density compared to that of solids or liquids.

(c) Gases exert pressure in all directions.

(d) It is necessary to specify the pressure and temperature of a gas while stating its volume.

(e) Inflating a balloon seems to violate Boyle's law.

(f) Mountaineers carry oxygen cylinders with them.

(g) Gas fills completely the vessel in which it is kept.

Answer

(a) The temperature -273°C is called absolute zero and it is theoretically the lowest temperature that can ever be achieved. The absolute (Kelvin) scale has its zero at -273°C. As temperatures lower than -273°C are not possible, hence, all temperatures in Kelvin scale are in positive figures.

(b) The number of molecules per unit volume in a gas is very small as compared to solids and liquids. Gases have large inter-molecular spaces between their molecules. Therefore gases have lower density compared to that of solids or liquids.

(c) The moving particles of a gas collide with each other and also with the walls of the container. Due to these collisions gas molecules exert pressure. It has been found that at a given temperature, time and area, the same number of molecules of a gas strike against the walls of the container. Thus, gases exert the same pressure in all directions.

(d) Since volume of a gas changes remarkably with change in temperature and pressure, it becomes necessary to choose standard values of temperature and pressure to which gas volumes can be referred.

(e) Boyle's law states that the volume of a dry gas is inversely proportional to its pressure at a constant temperature. When we inflate a balloon, the volume and pressure of the air increase simultaneously, seemingly violating Boyle's law. However, this is not the case because according to the law, the mass of the gas should remain constant. In the balloon scenario, as more air is blown into the balloon, the mass of the gas increases, ensuring Boyle's law is not violated.

(f) Atmospheric pressure is low at high altitudes, so air is less dense. Hence, lesser quantity of oxygen is available for breathing. Thus, mountaineers have to carry oxygen cylinders with them.

(g) Gas is a state of matter in which inter-particle attraction is weak and inter-particle space is so large that the particles become completely free to move randomly in the entire available space. Hence, it fills completely the vessel in which it is kept.

Exercise 7 — Descriptive Answer Type

Question 1

Give the assumptions of the kinetic molecular theory.

Answer

The assumptions of the kinetic molecular theory are :

1. Composition of gases — Gases are made of tiny particles moving in all possible directions at all possible speeds. The molecules are negligibly small as compared to the volume of the occupied gas.
2. Gases have neither a fixed volume nor a fixed shape — There is negligible force of attraction between the particles (gas molecules). Therefore, the particles (gas molecules) are free to move in the entire space available to them. Their movement is only restricted by the container, hence it takes the shape of the container.
3. Gases exert pressure in all directions — The moving particles of gas collide with each other and with the walls of the container. Due to these collisions, gas molecules exert pressure. It has been found, that at a given temperature, time and area, the same number of molecules of a gas strike against the walls of the container. Thus, gases exert the same pressure in all directions.
4. Gases are highly compressible — There are large inter-particle (inter-molecular) space between gas molecules, and this accounts for high compressibility of gases.
5. Gases are highly expansible — Gases increase in volume with a decrease in pressure and an increase in temperature.
6. Gases have low density — The number of molecules per unit volume in a gas is very small due to the large intermolecular spaces between their molecules. Therefore, gases have very low density.
7. Gases have a natural tendency for diffusion — Due to large intermolecular spaces, the molecules of two gases mix with each other in such a manner that a homogeneous gaseous mixture is formed.
8. Gases can be liquefied — On cooling, the kinetic energy of the molecules of a gas is reduced and on applying pressure on a cooled gas, the molecules come closer. Thus, the gas liquefies.

Question 2

Explain Boyle's law on the basis of the kinetic theory of matter.

Answer

According to the kinetic theory of gases, the number of particles and their average kinetic energy in a given mass of gas remain constant. When the volume of a gas is halved, the particles have less space to move, resulting in double the number of molecules striking the container walls per unit area and thus doubling the pressure. Conversely, doubling the volume gives the particles more space, reducing the number of molecules striking the walls per unit area by half and halving the pressure. This demonstrates Boyle's law: as pressure increases, the volume of a gas decreases at a constant temperature.

Question 3

Explain Charles' law on the basis of the kinetic theory of matter.

Answer

According to the kinetic theory of gases, the average kinetic energy of gas particles is directly proportional to the absolute temperature. Increasing the temperature causes the particles to move faster and strike the container walls more frequently and forcefully. When pressure is constant, the volume of the gas increases proportionally. Therefore, at constant pressure, the volume of a gas is directly proportional to its temperature (Charles' law).

Question 4

How did Charles' law lead to the concept of an absolute scale of temperature?

Answer

According to Charles' law, when pressure (P) is constant,

$\text{V} = \text{V}_0 + \dfrac{\text{V}_0}{273}\text{t} \\[1em] \Rightarrow \text{V} = \text{V}_0\Big(\dfrac{273 + \text{t}}{273}\Big)$

∴ Volume at -273°C = $\text{V}_0\Big(\dfrac{273 - 273}{273}\Big)$ = 0

Hence, the volume of a gas would be reduced to zero at -273°C. This temperature is called absolute zero.

This allowed the scientists to establish an absolute temperature scale (known as Kelvin scale) by defining absolute zero as the point where volume of a gas would theoretically be zero.

Question 5

(a) State Boyle's Law.

(b) Give its

(i) mathematical expression,

(ii) graphical representation and

(iii) significance.

Answer

(a) Boyle's law states that the volume of a given mass of a dry gas is inversely proportional to its pressure at a constant temperature.

(b) (i) Mathematical expression of Boyle's law :

Suppose a gas occupies volume V₁ when its pressure is P₁; then

V₁ α $\dfrac{1}{\text{P}_1}$ or

V₁ = $\dfrac{\text{k}}{\text{P}_1}$ or

P₁V₁ = k = constant

If V₂ is the volume occupied when the pressure is P₂ at the same temperature, then

V₂ α $\dfrac{1}{\text{P}_2}$ or

V₂ = $\dfrac{\text{k}}{\text{P}_2}$ or

P₂V₂ = k = constant

∴ P₁V₁ = P₂V₂ = k; at constant temperature.

(ii) Graphical representation of Boyle's Law:

(a) V vs $\dfrac{1}{\text{P}}$ : a straight line passing through the origin is obtained.

(b) V vs P : a hyperbolic curve in the first quadrant is obtained.

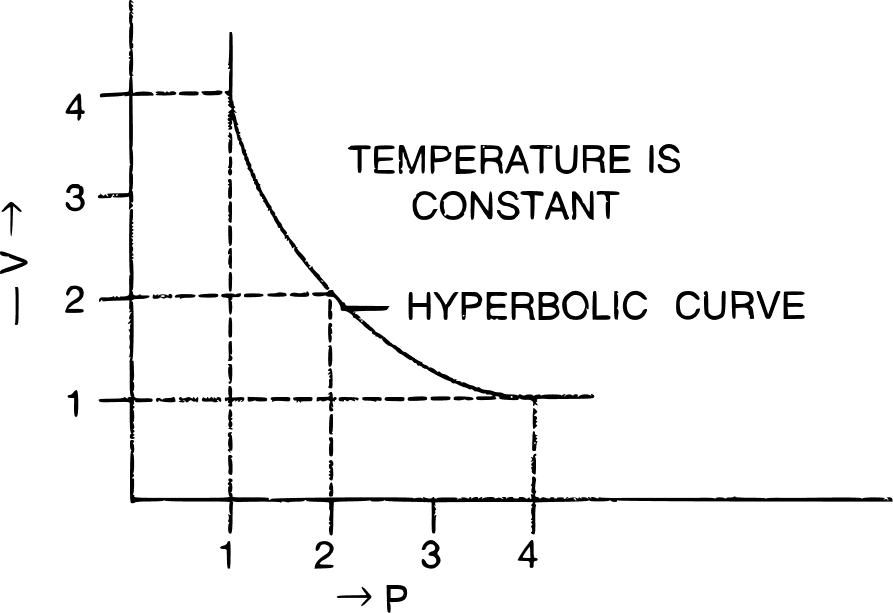
(c) PV vs P : a straight line is obtained parallel to the pressure axis.

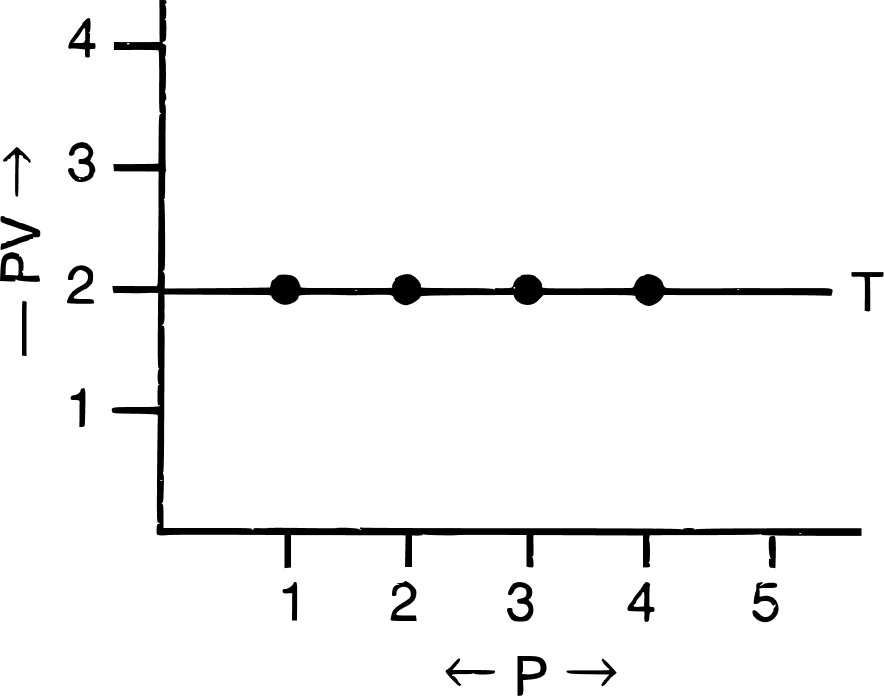
(iii) Significance of Boyle's law :
On increasing pressure, volume decreases. The gas becomes denser. Thus, at constant temperature, the density of a gas is directly proportional to pressure.

Question 6

(a) State Charles' law.

(b) Give its

(i) Graphical representation,

(ii) mathematical expression and

(iii) Significance.

Answer

(a) Charles law states that pressure remaining constant, the volume of a given mass of dry gas increases or decreases by $\dfrac{1}{273}$ of its volume at 0°C for each 1°C increase or decrease in temperature, respectively.

(b) (i) Graphical representation of Charles' law : The relationship between the volume and the temperature of a gas can be plotted on a graph. A straight line is obtained.

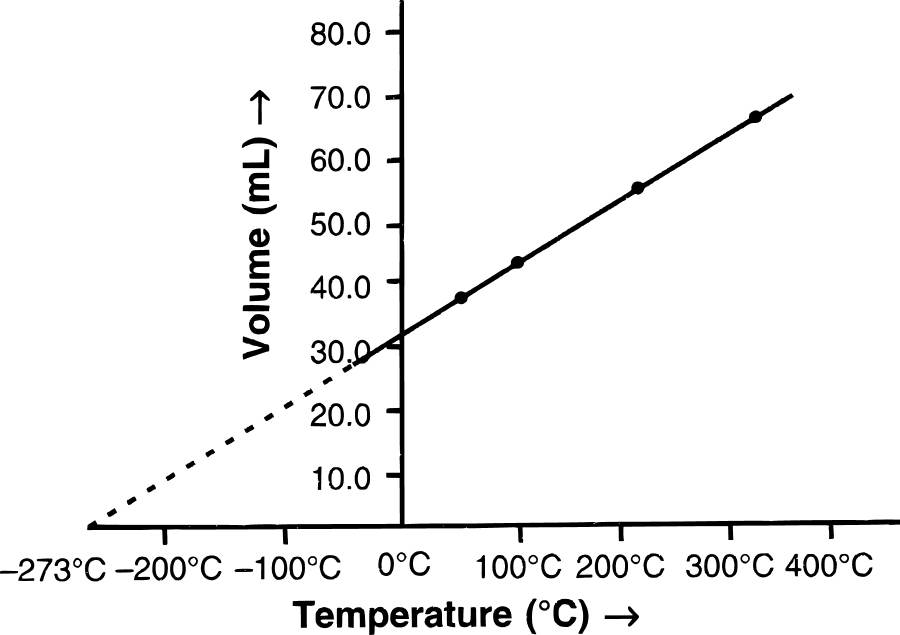
(ii) Mathematical expression of Charles' law :

Suppose, a gas occupies V₁ cm³ at T₁ temperature and V₂ cm³ at T₂ temperature, then by Charles' law:

    V₁ α T₁

or V₁ = kT₁ (k is constant)

or $\dfrac{\text{V}_1}{\text{T}_1}$ = k and

    V₂ α T₂

or $\dfrac{\text{V}_2}{\text{T}_2}$ = k

∴ $\dfrac{\text{V}_1}{\text{T}_1}$ = $\dfrac{\text{V}_2}{\text{T}_2}$ = k (at constant pressure)

(iii) Significance of Charles' Law :
Volume of a given mass of a gas is directly proportional to its temperature, hence, density decreases with an increase in temperature.

Question 7

What is meant by aqueous tension? How is the pressure exerted by a gas corrected to account for aqueous tension?

Answer

When the gas is collected over water, it is moist and contains water vapour. The total pressure exerted by moist gas is equal to the sum of the partial pressure of the dry gas and the pressure exerted by water vapour. The partial pressure of water vapour is called as aqueous tension.

P_total = P_gas + P_{water vapour}

P_gas = P_total – P_{water vapour}

Actual pressure of gas = Total pressure – Aqueous tension

Thus, to obtain the actual pressure, the pressure which is due to moisture in the gas has to be subtracted.

Question 8

During the chemistry practical when hydrogen sulphide gas having offensive odour is prepared for some test in the laboratory, we can smell the gas from even 50 metres away. Explain the phenomenon.

Answer

The phenomenon is Diffusion.

Diffusion is the process of gradual mixing of two substances, kept in contact, by molecular motion.

The molecules of hydrogen sulphide gas collide with air particles and due to the collisions of the particles, they start moving in a haphazard manner in all possible directions. Due to this, the molecules of hydrogen sulphide gas quickly spread in the surroundings and we can smell the gas from even 50 metres away.

Exercise 7 — Structured/Application/Skill Type

Question 1

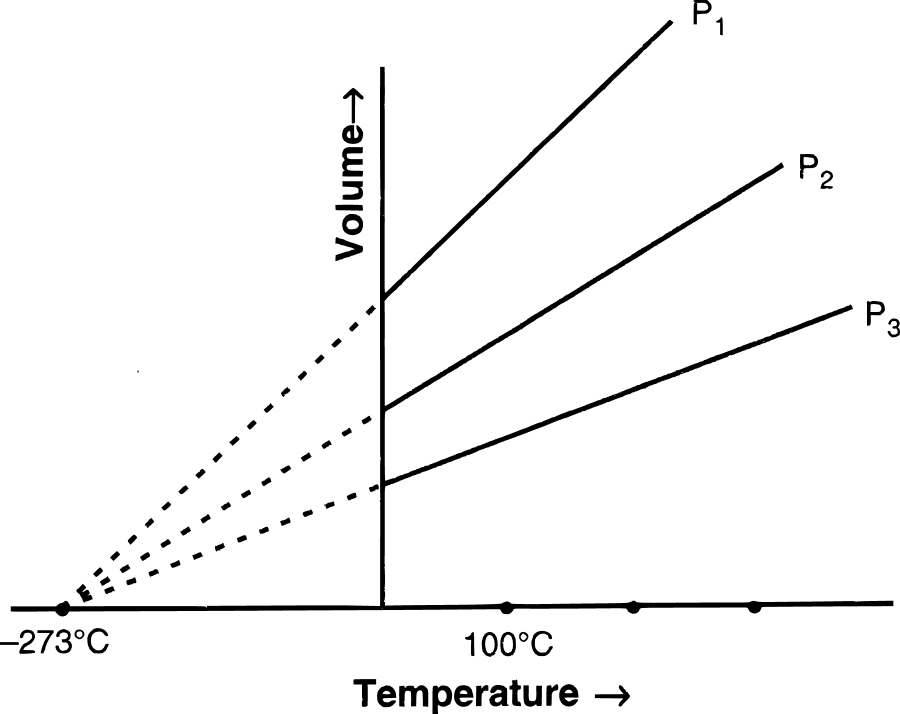
(a) State the law verified by the following figure:

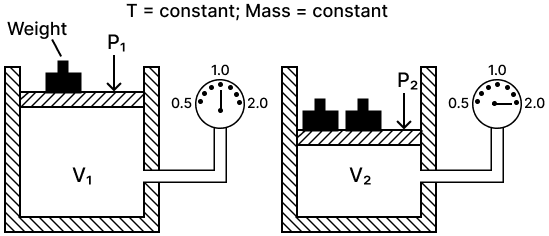
(b) Draw P.V. isothermal for the above law.

Answer

(a) Boyle's law — It states that the volume of a given mass of a dry gas is inversely proportional to its pressure at a constant temperature i.e., P₁V₁ = P₂V₂

(b) P.V. isothermal for Boyle's law is shown below :

Question 2

(a) State the law which the following graph verifies.

(b) Derive the mathematical expression for it.

(c) Give one application/use where the above law is employed.

Answer

(a) Charles' law — It states that pressure remaining constant, the volume of a given mass of dry gas increases or decreases by $\dfrac{1}{273}$ of its volume at 0°C for each 1°C increase or decrease in temperature, respectively.

(b) Let V₀ be the volume of a fixed mass of a gas at 0°C and let V be its volume at temperature t°C at constant pressure. Then according to Charles' law,

V = V_o + $\dfrac{\text{V}_0}{273}$t (when P is constant)

V = V_o (1 + $\dfrac{\text{t}}{273}$)

= V_o ($\dfrac{\text{273 + t}}{273}$)

V = $\dfrac{\text{V}_0}{273}$T where T = 273 + t

For a given mass of a gas,

$\dfrac{\text{V}_0}{273}$ = constant

∴ V = k x T (where k is constant)

or V α T and $\dfrac{\text{V}}{\text{T}}$ = K

Suppose a gas occupies V₁ cm³ at T₁ temperature and V₂ cm³ at T₂ temperature, then by Charles law,

    V₁ α T₁

or V₁ = kT₁ (k is constant)

or $\dfrac{\text{V}_1}{\text{T}_1}$ = k and

    V₂ α T₂

or $\dfrac{\text{V}_2}{\text{T}_2}$ = k

∴ $\dfrac{\text{V}_1}{\text{T}_1}$ = $\dfrac{\text{V}_2}{\text{T}_2}$ = k (at constant pressure)

(c) Volume of a given mass of a gas is directly proportional to its temperature, hence, density decreases with an increase in temperature. This is the reason that hot air is filled into balloons used for meteorological purposes.

Question 3

Plot V versus absolute T (K) by the given data:

(a) The graph between V and T is a ............... .

(b) Check whether the line passes through the origin.

(c) Which law is obeyed.

Answer

Converting temperature to Kelvin Scale :

Graph of V versus absolute T is shown below :

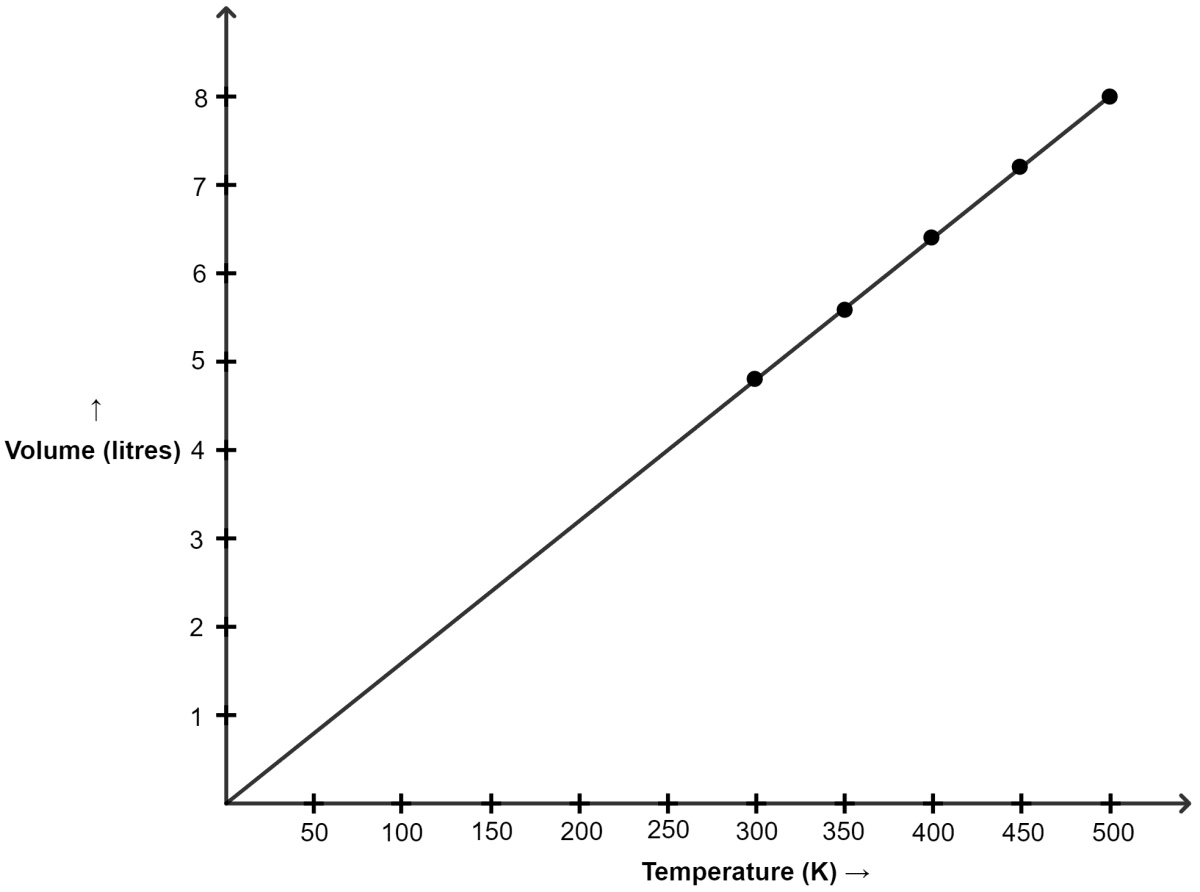
(a) The graph between V and T is a straight line.

(b) Yes, as we can see in the graph, the line passes through the origin.

(c) Charles' law

Exercise 7 — Numericals

Question 1

Convert :

(i) 273°C to kelvin

(ii) 293 K to °C

Answer

(i) Kelvin = °C + 273 = 273 + 273 = 546 K

(ii) °C = Kelvin - 273 = 293 - 273 = 20°C

Question 2

What will be the minimum pressure required to compress 500 dm³ of air at 1 bar to 200 dm³, if temperature is kept constant?

Answer

Given,

V₁ = Initial volume of the gas = 500 dm³
P₁ = Initial pressure of the gas = 1 bar.
V₂ = Final volume = 200 dm³
P₂ = Final pressure of the gas = ?

By Boyle's Law:

$\text{P}_1 \text{V}_1 = \text{P}_2 \text{V}_2$

Substituting the values :

$1 \times 500 = \text{P}_2 \times 200 \\[0.5em] \text{P}_2 = \dfrac{500}{200} \\[0.5em] \text{P}_2 = 2.5 \text{ bar }$

∴ Final pressure of the gas = 2.5 bar.

Question 3

2 litres of a gas is enclosed in a vessel at a pressure of 760 mm Hg. If temperature remains constant, calculate pressure when volume changes to 4 dm³.

Answer

V₁ = 2 lits.

P₁ (Initial pressure) = 760 mm Hg

V₂ = 4 dm³

P₂ (Final pressure) = ?

By Boyle's Law:

$\text{P}_1 \text{V}_1 = \text{P}_2 \text{V}_2$

Substituting the values :

$760 \times 2 = \text{P}_2 \times 4 \\[1em] \text{P}_2 = \dfrac{760 \times 2}{4} \\[1em] \text{P}_2 = 380 \text{ mm Hg}$

∴ Final pressure of the gas = 380 mm Hg.

Question 4

800 cm³ of gas is collected at 654 mm pressure. At what pressure would the volume of the gas reduce by 40% of its original volume, temperature remaining constant?

Answer

V₁ = 800 cm³

P₁ (Initial pressure) = 654 mm of Hg

V₂ = reduces by 40% of it's initial value

= 800 - ($\dfrac{40}{100}$ x 800)

= 800 - 320 = 480 cm³

P₂ (Final pressure) = ?

By Boyle's Law:

$\text{P}_1 \text{V}_1 = \text{P}_2 \text{V}_2$

Substituting the values :

$654 \times 800 = \text{P}_2 \times 480 \\[1em] \text{P}_2 = \dfrac{800 \times 654}{480} \\[1em] \text{P}_2 = 1090 \text{ mm of Hg}$

∴ Final pressure of the gas = 1090 mm of Hg.

Question 5

At constant temperature, the effect of change of pressure on volume of a gas was as given below :

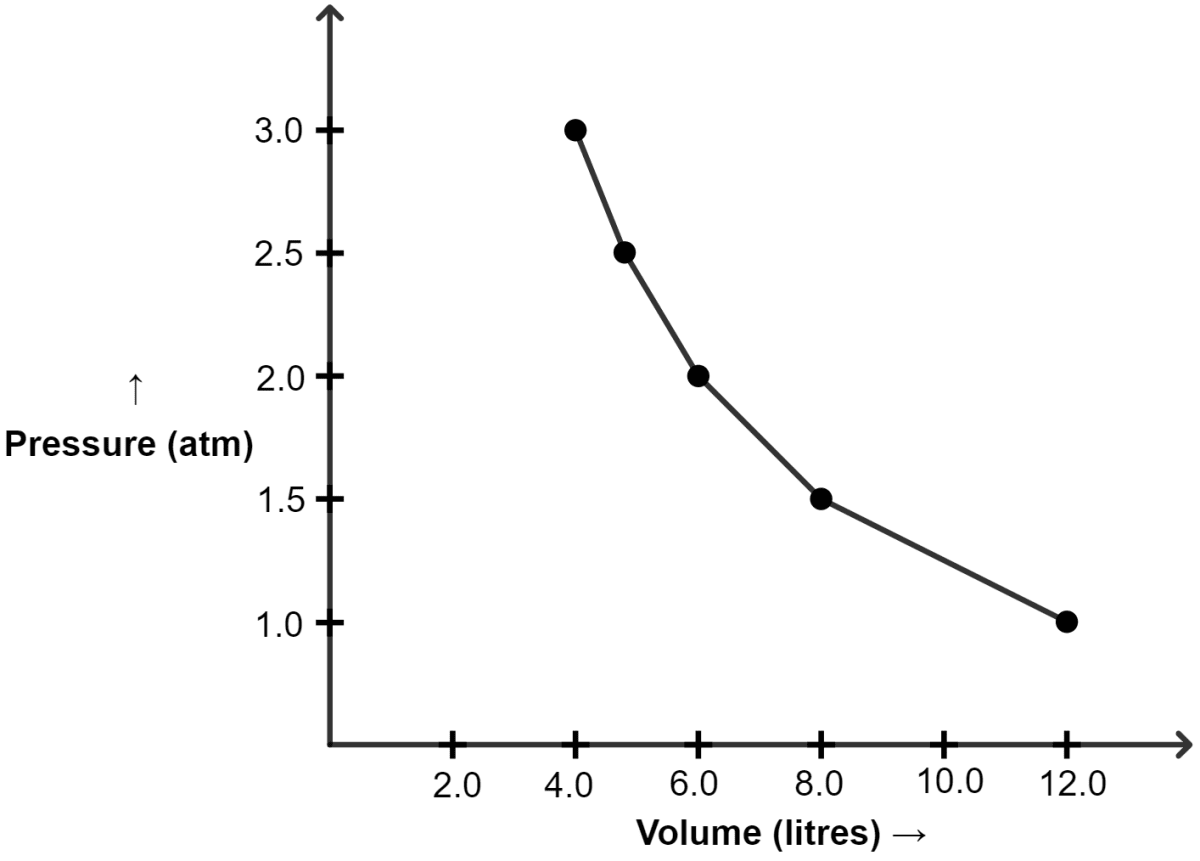
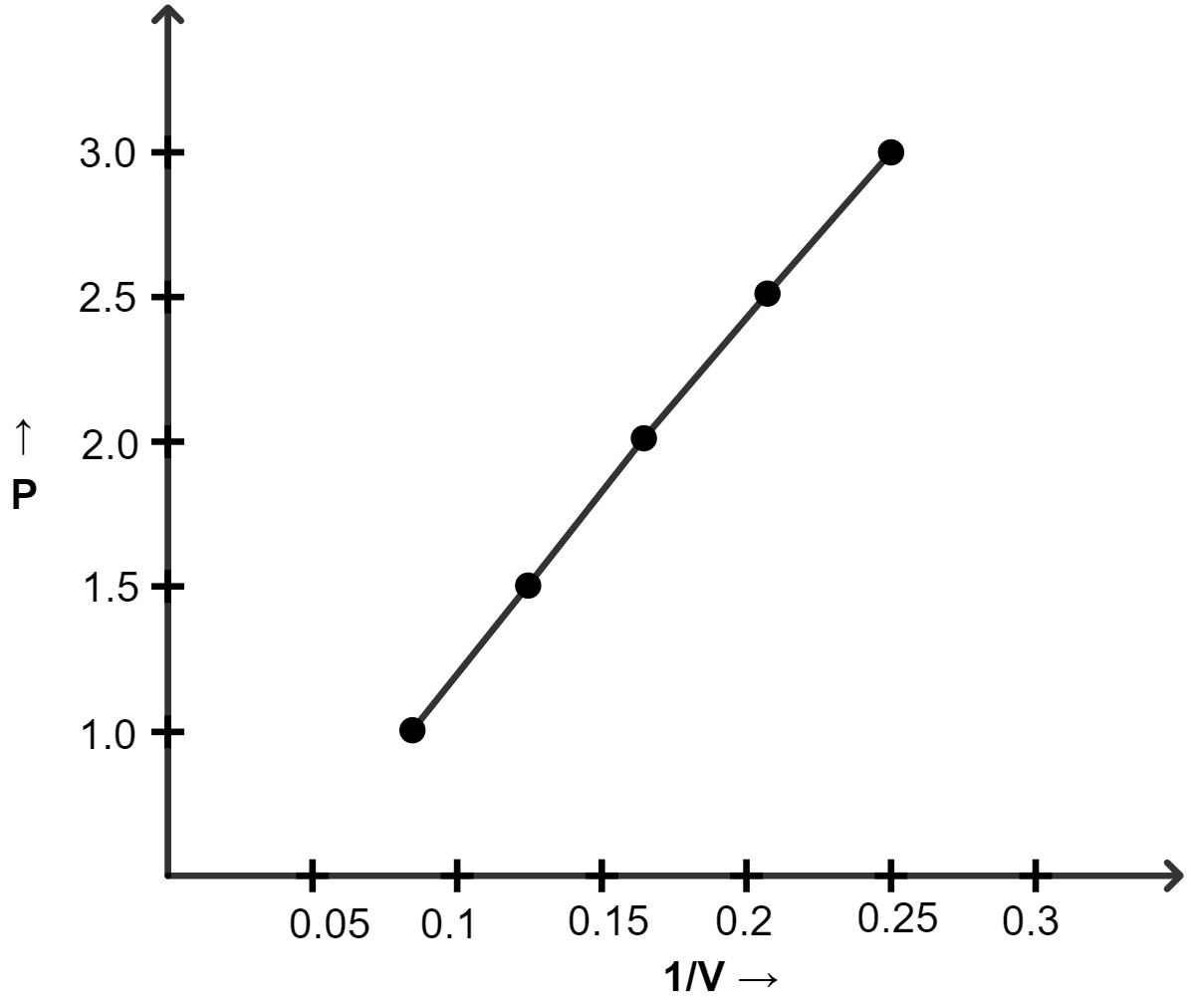
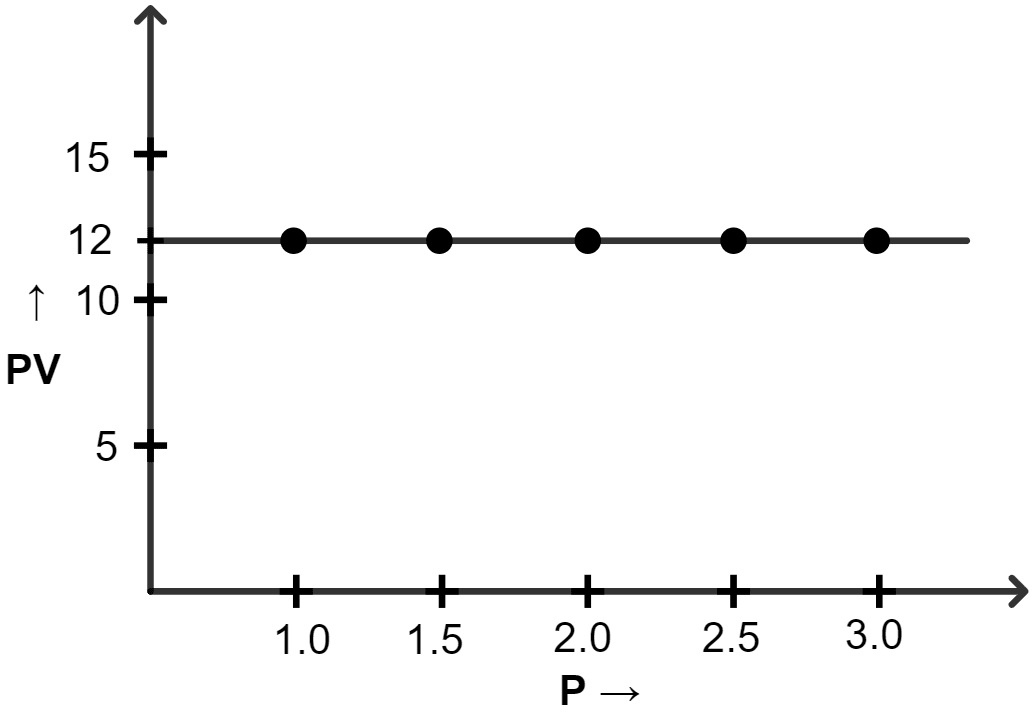
(a) Plot the following graphs :

(i) P vs V

(ii) P vs 1/V

(iii) PV vs P

(b) Assuming that the pressure values given above are correct, find the correct measurement of the volume at 2.3 atmosphere pressure.

Answer

(a)

(i) Graph of P vs V :

(ii) Graph of P vs 1/V :

(iii) Graph of PV vs P :

(b) By Boyle's Law:

$\text{P}_1 \text{V}_1 = \text{P}_2 \text{V}_2$

P₁V₁ = 12 is a constant, hence, V₂ = ? at P₂ = 2.3 atm

Substituting the values :

$12 = 2.3 \times \text{V}_2 \\[1em] \text{V}_2 = \dfrac{12}{2.3} \\[1em] \text{V}_2 = 5.217 \text{ lit}$

Hence, volume = 5.217 lit

Question 6

A cylinder of 20 litres capacity contains a gas at 100 atmospheric pressure. How many flasks of 200 cm³ capacity can be filled from it at 1 atmosphere pressure temperature remaining constant?

Answer

V₁ = 20 lits.

1 lit. = 1000 cm³

∴ 20 lit = 20,000 cm³

P₁ (Initial pressure) = 100 atmos.

P₂ (Final pressure) = 1 atmos.

V₂ = ?

By Boyle's Law:

$\text{P}_1 \text{V}_1 = \text{P}_2 \text{V}_2$

Substituting the values :

$100 \times 20,000 = 1 \times \text{V}_2 \\[0.5em] \text{V}_2 = 20,00,000 \text{ cm}^3$

200 cm³ = capacity of 1 flask
∴ Number of flasks required for 20,00,000 cm³ of gas

$= \dfrac{20,00,000 }{200} = 10,000$

Hence, number of flask that can be filled = 10,000.

Question 7

A steel cylinder of internal volume 20 litres is filled with hydrogen at 29 atmospheric pressure. If hydrogen is used to fill a balloon at 1.25 atmospheric pressure at the same temperature, what volume will the gas occupy ?

Answer

V₁ = 20 litres

P₁ = 29 atmospheric pressure

P₂ = 1.25 atmospheric pressure

V₂ = ?

By Boyle's Law:

$\text{P}_1 \text{V}_1 = \text{P}_2 \text{V}_2$

Substituting the values :

$20 \times 29 = 1.25 \times \text{V}_2 \\[0.5em] \text{V}_2 = \dfrac{20\times 29}{1.25} \\[0.5em] \text{V}_2 = 464 \text{ litres}$

∴ Volume occupied = 464 litres.

Question 8

561 dm³ of a gas at S.T.P. is filled in a 748 dm³ container. If temperature is constant, calculate the percentage change in pressure required.

Answer

V₁ = 561 dm³

P₁ = P

V₂ = 748 dm³

P₂ = ?

By Boyle's Law:

$\text{P}_1 \text{V}_1 = \text{P}_2 \text{V}_2$

Substituting the values :

$561 \times \text{P} = 748 \times \text{P}_2 \\[1em] \text{P}_2 = \dfrac{561\times \text{P}}{748} \\[1em] \text{P}_2 = 0.75 \text{P}$

Change in pressure = P - 0.75P = 0.25P decrease

Percentage decrease in pressure = $\dfrac{\text{Decrease}}{\text{Original}}$ x 100 = $\dfrac{\text{0.25P}}{\text{P}}$ x 100 = 25%

∴ Percentage decrease in the pressure of the gas = 25%

Question 9

88 cm³ of nitrogen is at a pressure of 770 mm mercury. If the pressure is raised to 880 mm Hg, find by how much the volume will diminish, temperature remains constant.

Answer

V₁ = 88 cm³

P₁ = 770 mm

P₂ = 880 mm Hg

V₂ = ?

By Boyle's Law:

$\text{P}_1 \text{V}_1 = \text{P}_2 \text{V}_2$

Substituting the values :

$770 \times 88 = 880 \times \text{V}_2 \\[0.5em] \text{V}_2 = \dfrac{770 \times 88}{880} \\[0.5em] \text{V}_2 = 77$

V₂ = 77 cm³

∴ Decrease in volume = 88 - 77 = 11 cm³

Question 10

A gas at 240 K is heated to 127°C. Find the percentage change in the volume of the gas (pressure remaining constant).

Answer

V₁ = Initial volume of the gas = V cc
T₁ = Initial temperature of the gas = 240 K
T₂ = Final temperature of the gas = 127°C = 127 + 273 = 400 K
V₂ = Final volume of the gas = ?

By Charles' Law:

$\dfrac{\text{V}_1}{\text{T}_1} = \dfrac{\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{\text{V}}{240} = \dfrac{\text{V}_2}{400} \\[1em] \text{V}_2 = \dfrac{400 \times \text{V}}{240} \\[1em] \text{V}_2 = \dfrac{5\times \text{V}}{3}$

Increase in vol. = $\dfrac{5\text{V}}{3}$ - V = $\dfrac{2\text{V}}{3}$

Percentage increase in vol. = $\dfrac{\text{Increase}}{\text{Original}}$ x 100 = $\dfrac{2\text{V}}{3\text{V}}$ x 100 = 66.67%

∴ Percentage increase in the volume of the gas = 66.67%

Question 11

Certain amount of a gas occupies a volume of 0.4 litre at 17°C. To what temperature should it be heated so that its volume gets (a) doubled (b) reduced to half, pressure remaining constant?

Answer

(a) To find the temperature so that volume gets doubled :

V₁ = Initial volume of the gas = 0.4 litre
T₁ = Initial temperature of the gas = 17°C = 17 + 273 = 290 K
V₂ = Final volume of the gas = double of initial = 2 x 0.4 = 0.8 litre
T₂ = Final temperature of the gas = ?

By Charles' Law:

$\dfrac{\text{V}_1}{\text{T}_1} = \dfrac{\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{\text{0.4}}{290} = \dfrac{\text{0.8}}{\text{T}_2} \\[1em] \text{T}_2 = \dfrac{0.8 \times 290}{0.4} \\[1em] \text{T}_2 = 580 \text{ K}$

∴ Final temperature in °C = 580 - 273 = 307°C

(b) To find the temperature so that volume gets reduced to half :

V₁ = Initial volume of the gas = 0.4 litre
T₁ = Initial temperature of the gas = 17°C = 17 + 273 = 290 K
V₂ = Final volume of the gas = reduced to half of initial = 0.2 litre
T₂ = Final temperature of the gas = ?

By Charles' Law:

$\dfrac{\text{V}_1}{\text{T}_1} = \dfrac{\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{\text{0.4}}{290} = \dfrac{\text{0.2}}{\text{T}_2} \\[1em] \text{T}_2 = \dfrac{0.2\times 290}{0.4} \\[1em] \text{T}_2 = 145$

∴ Final temperature in °C = 145 - 273 = -128°C

Question 12

A given mass of a gas occupies 143 cm³ at 27°C and 700 mm Hg pressure. What will be its volume at 300 K and 280 mm Hg pressure?

Answer

By Gas Law:

$\dfrac{\text{P}_1\times\text{V}_1}{\text{T}_1} = \dfrac{\text{P}_2\times\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{700 \times 143}{300} = \dfrac{280\times\text{\text{V}}_2}{300} \\[1em] \text{V}_2 =\dfrac{700 \times 143 }{280} \\[1em] \text{V}_2 = 357.5 \text{ cm}^3$

∴ Final volume of the gas = 357.5 cm³

Question 13

A gas occupies 500 cm³ at S.T.P. At what temperature will the volume of the gas be reduced by 20% of its original volume, pressure being constant?

Answer

V₁ = Initial volume of the gas = 500 cm³
T₁ = Initial temperature of the gas = 273 K
V₂ = Final volume of the gas = reduced by 20% of its original = 500 - ($\dfrac{20}{100}$ x 500) = 500 - 100 = 400 cm³
T₂ = Final temperature of the gas = ?

By Charles' Law:

$\dfrac{\text{V}_1}{\text{T}_1} = \dfrac{\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{500}{273} = \dfrac{400}{\text{T}_2} \\[1em] \text{T}_2 = \dfrac{400 \times 273}{500} \\[1em] \text{T}_2 = 218.4 \text{ K}$

Final temperature = 218.4 K

Question 14

Calculate the final volume of a gas 'X', if the original pressure of the gas, at S.T.P. is doubled and its temperature is increased three times.

Answer

By Gas Law:

$\dfrac{\text{P}_1\times\text{V}_1}{\text{T}_1} = \dfrac{\text{P}_2\times\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{760 \times \text{V}}{273} = \dfrac{ 2 \times 760 \times\text{\text{V}}_2}{3 \times 273} \\[1em] \text{V}_2 =\dfrac{3 }{2}\text{V} \\[1em] \text{V}_2 = 1\dfrac{1}{2} \text{V}$

∴ Final volume of the gas = $1\dfrac{1}{2}$ times the original volume.

Question 15

A sample of carbon dioxide occupies 30 cm³ at 15°C and 740 mm pressure. Find its volume at S.T.P.

Answer

By Gas Law:

$\dfrac{\text{P}_1\times\text{V}_1}{\text{T}_1} = \dfrac{\text{P}_2\times\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{740 \times 30}{288} = \dfrac{ 760 \times\text{\text{V}}_2}{273} \\[1em] \text{V}_2 =\dfrac{740 \times 30\times 273}{288 \times 760} \\[1em] \text{V}_2 = 27.68 \text{ cm}^3$

∴ Volume of carbon dioxide = 27.7 cm³

Question 16

What temperature would be necessary to double the volume of a gas, initially at S.T.P., if the pressure is decreased to 50% ?

Answer

By Gas Law:

$\dfrac{\text{P}_1\times\text{V}_1}{\text{T}_1} = \dfrac{\text{P}_2\times\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{1\times \text{V}}{273} = \dfrac{0.5\times\text{2\text{V}}}{\text{T}_2} \\[0.5em] \text{T}_2 = 0.5\times 2 \times 273\\[0.5em] \text{T}_2 = 273\text{ K}$

∴ Final temperature of the gas = 273 K

Question 17

At 0°C and 760 mm Hg pressure, a gas occupies volume of 100 cm³. Kelvin temperature of the gas is increased by one-fifth and the pressure is increased one and a half times. Calculate the final volume of the gas.

Answer

Initial conditions [S.T.P.] :

P₁ = Initial pressure of the gas = 760 mm Hg
V₁ = Initial volume of the gas = 100 cm³
T₁ = Initial temperature of the gas = 0°C = 273 K

Final conditions :

P₂ (Final pressure) = increased one and a half times of P₁

= (1 + $\dfrac{1}{2}$) of 760

= $\dfrac{3}{2}$ x 760

= 3 x 380

= 1140 mm Hg

V₂ (Final volume) = ?

T₂ (Final temperature) = increased by one-fifth of 273 K

= $\Big(1 + \dfrac{1}{5}\Big)$ of 273

= $\dfrac{6}{5}$ x 273 = $\dfrac{1638}{5}$

By Gas Law:

$\dfrac{\text{P}_1\times\text{V}_1}{\text{T}_1} = \dfrac{\text{P}_2\times\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{760 \times 100 }{273} = \dfrac{1140 \times \text{V}_2}{\dfrac{1638}{5}} \\[1em] \dfrac{760 \times 100 }{273} = \dfrac{5 \times 1140 \times \text{V}_2}{1638} \\[1em] \text{V}_2 = \dfrac{760 \times 100 \times 1638}{273 \times 5 \times 1140} \\[1em] \text{V}_2 = 80 \text{ cm}^3$

∴ Final volume of the gas = 80 cm³

Question 18

It is found, on heating a gas, its volume increases by 50% and pressure decreases to 60% of its original value. If the original temperature was -15°C, find the temperature to which it was heated?

Answer

Initial conditions [S.T.P.] :

P₁ = Initial pressure of the gas = P
V₁ = Initial volume of the gas = V
T₁ = Initial temperature of the gas = -15°C = -15 + 273 = 258 K

Final conditions :

P₂ (Final pressure) = pressure decreases to 60% of its original value

= $\dfrac{60}{100}$ of P

= $\dfrac{3}{5}$P

V₂ (Final volume) = volume increases by 50% of its original value

= 1 + $\dfrac{50}{100}$ of V

= $\dfrac{100 + 50}{100}$ of V

= $\dfrac{150}{100}$ of V

= $\dfrac{3}{2}$V

T₂ (Final temperature) = ?

By Gas Law:

$\dfrac{\text{P}_1\times\text{V}_1}{\text{T}_1} = \dfrac{\text{P}_2\times\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{\text{PV }}{258} = \dfrac{\dfrac{3}{5} \text{P}\times\dfrac{3}{2}\text{V}}{\text{T}_2} \\[1em] \text{T}_2 = \dfrac{3\times 3\times 258}{5 \times 2} = \dfrac{2322}{10} \\[1em] \text{T}_2 = 232.2 \text{K} \\[1em]$

∴ Final temperature of the gas = 232.2 - 273 = -40.8°C

Question 19

A certain mass of a gas occupies 2 Litres at 27°C and 100 pascal. Find the temperature when volume and pressure become half of their initial values.

Answer

Initial conditions [S.T.P.] :

P₁ = Initial pressure of the gas = 100 Pascal

V₁ = Initial volume of the gas = 2 Litres

T₁ = Initial temperature of the gas = 27°C = 27 + 273 = 300 K

Final conditions :

P₂ (Final pressure) = 50 Pascal
V₂ (Final volume) = 1 litre
T₂ (Final temperature) = ?

By Gas Law:

$\dfrac{\text{P}_1\times\text{V}_1}{\text{T}_1} = \dfrac{\text{P}_2\times\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{100 \times 2}{300} = \dfrac{50 \times 1}{\text{T}_2} \\[1em] \text{T}_2 = \dfrac{50\times 3}{2} \\[1em] \text{T}_2 = 75 \text{K} \\[1em]$

∴ Final temperature of the gas = 75 - 273 = -198°C

Question 20

2500 cm³ of hydrogen is taken at S.T.P. The pressure of this gas is further increased by two and and a half times (temperature remaining constant). What volume will hydrogen occupy now?

Answer

V₁ = 2500 cm³

P₁ = 760 mm Hg

P₂ = increased by two and a half times

= (1 + $2\dfrac{1}{2}$ ) times of 760 mm Hg

= (1 + $\dfrac{5}{2}$ ) times of 760 mm Hg

= ( $\dfrac{7}{2}$ x 760) mm Hg

V₂ = ?

By Boyle's Law:

$\text{P}_1 \text{V}_1 = \text{P}_2 \text{V}_2$

Substituting the values :

$760 \times 2500 = \dfrac{7}{2} \times 760 \times \text{V}_2 \\[1em] \text{V}_2 = \dfrac{5000}{7} \\[0.5em]$

∴ Final volume = $\dfrac{5000}{7}$ cm³

Question 21

Taking the volume of hydrogen as calculated in Q.20 what change must be made in Kelvin (absolute) temperature to return the volume to 2500 cm³ (pressure remaining constant).

Answer

V₁ = Initial volume of the gas = $\dfrac{5000}{7}$ cm³
T₁ = Initial temperature of the gas = 273 K

V₂ = Final volume of the gas = 2500 cm³
T₂ = Final temperature of the gas = ?

By Charles' Law:

$\dfrac{\text{V}_1}{\text{T}_1} = \dfrac{\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{5000}{7 \times 273} = \dfrac{2500}{\text{T}_2} \\[1em] \text{T}_2 = \dfrac{7 \times 273 \times 2500}{5000} \\[1em] \text{T}_2 = \dfrac{7 \times 273}{2} \\[1em] \text{T}_2 = 3.5 \times 273 \\[1em]$

∴ Final temperature = 3.5 times of Kelvin temperature.

Question 22

A given amount of gas A is confined in a chamber of constant volume. When the chamber is immersed in a bath of melting ice, the pressure of the gas is 100 cm Hg.

(a) What is the temperature, when the pressure is 10 cm Hg?

(b) What will be the pressure, when the chamber is brought to 100°C?

Answer

(a) P₁ = Initial pressure of the gas = 100 cm Hg

T₁ = Initial temperature of the gas = 273 K

P₂ = Final pressure of the gas = 10 cm Hg

T₂ = Final temperature of the gas = ?

V₁ = V₂ = V [constant volume]

By Gas Law:

$\dfrac{\text{P}_1\times\text{V}_1}{\text{T}_1} = \dfrac{\text{P}_2\times\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{100 \times \text{V}}{273} = \dfrac{10 \times \text{V}}{\text{T}_2} \\[1em] \text{T}_2 = \dfrac{ 273}{10} \\[1em] \text{T}_2 = 27.3 \text {K} \\[1em]$

∴ When the pressure is 10 cm Hg, the temperature is 27.3 K.

(b) P₁ = Initial pressure of the gas = 100 cm Hg

T₁ = Initial temperature of the gas (ice point) = 273 K

P₂ = Final pressure of the gas = ?

T₂ = Final temperature of the gas = 100°C = 273 + 100 = 373 K

V₁ = V₂ = V [constant volume]

By Gas Law:

$\dfrac{\text{P}_1\times\text{V}_1}{\text{T}_1} = \dfrac{\text{P}_2\times\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{100 \times \text{V}}{273} = \dfrac{\text{P}_2 \times \text{V}}{373} \\[1em] \text{P}_2 = \dfrac{ 37300}{273} \\[1em] \text{P}_2 = 136.63 \text { cm of Hg} \\[1em]$

∴ When the chamber is brought to 100°C, the pressure is 136.63 cm Hg.

Question 23

A gas is to be filled from a tank of capacity 10,000 litres into cylinders each having capacity of 10 litres. The condition of the gas in the tank is as follows:

(a) pressure inside the tank is 800 mm of Hg.

(b) temperature inside the tank is -3°C.

When the cylinder is filled, the pressure gauge reads 400 mm of Hg and the temperature is 270 K. Find the number of cylinders required to fill the gas.

Answer

Initial conditions :

P₁ = Initial pressure of the gas = 800 mm of Hg

V₁ = Initial volume of the gas = 10,000 litres

T₁ = Initial temperature of the gas = -3°C = -3 + 273 = 270 K

Final conditions:

P₂ (Final pressure) = 400 mm of Hg

V₂ (Final volume) = 10 litres x n cylinders

T₂ (Final temperature) = 270 K

where n is the number of cylinders = ?

By Gas Law:

$\dfrac{\text{P}_1\times\text{V}_1}{\text{T}_1} = \dfrac{\text{P}_2\times\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{800 \times 10,000}{270} = \dfrac{400 \times 10 \times n}{270} \\[1em] \text{n} = \dfrac{800 \times 10,000 \times 270}{400 \times 10 \times 270} \\[1em] \text{n} = \dfrac{800\times 10}{4} \\[1em] \text{n} = 2000 \\[1em]$

∴ Number of cylinders = 2000.

Question 24

A sealed tube (able to withstand a pressure of 3 atmospheres) is filled with air at 27°C and one atmosphere pressure. Find the temperature above which it will burst.

Answer

P₁ = Initial pressure of the gas = 1 atm

T₁ = Initial temperature of the gas = 27°C = 27 + 273 = 300 K

P₂ = Final pressure of the gas = 3 atm

T₂ = Final temperature of the gas = ?

V₁ = V₂ = V [constant volume]

By Gas Law:

$\dfrac{\text{P}_1\times\text{V}_1}{\text{T}_1} = \dfrac{\text{P}_2\times\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{1\times\text{V}}{300} = \dfrac{3\times\text{V}}{\text{T}_2} \\[1em] \text{T}_2 = 3 \times 300\\[1em] \text{T}_2 = 900 \text {K} \\[1em]$

∴ The temperature above which the tube will burst is 627°C.

Question 25

Calculate the temperature at which the volume of a gas is doubled if its pressure at the same time increases from 70 cm of Hg to 80 cm of Hg.

Answer

Initial conditions :

P₁ = Initial pressure of the gas = 70 cm of Hg

V₁ = Initial volume of the gas = V

T₁ = Initial temperature of the gas = 273 K

Final conditions:

P₂ (Final pressure) = 80 cm of Hg

V₂ (Final volume) = 2V

T₂ (Final temperature) = ?

By Gas Law:

$\dfrac{\text{P}_1\times\text{V}_1}{\text{T}_1} = \dfrac{\text{P}_2\times\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{70 \times \text{V}}{273} = \dfrac{80 \times \text{2V}}{\text{T}_2} \\[1em] \text{T}_2 = \dfrac{80 \times \text{2V} \times 273}{70 \times \text{V}} \\[1em] \text{T}_2 = \dfrac{16 \times 273}{7} \\[1em] \text{T}_2 = 624 \text{ K} \\[1em]$

∴ Final temperature of the gas = 624 - 273 = 351°C

Question 26

Calculate the volume occupied by 2 g of hydrogen at 27°C and 4 atmosphere pressure, if at S.T.P. it occupies 22.4 litres.

Answer

Initial conditions [S.T.P.] :

P₁ = Initial pressure of the gas = 1 atm

V₁ = Initial volume of the gas = 22.4 l

T₁ = Initial temperature of the gas = 273 K

Final conditions :

P₂ (Final pressure) = 4 atm

T₂ (Final temperature) = 27°C = 27 + 273 = 300 K

V₂ (Final volume) = ?

By Gas Law:

$\dfrac{\text{P}_1\times\text{V}_1}{\text{T}_1} = \dfrac{\text{P}_2\times\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{1 \times 22.4}{273} = \dfrac{4 \times \text{V}_2}{300} \\[1em] \text{V}_2 = \dfrac{300 \times 22.4}{273 \times 4} \\[1em] \text{V}_2 = 6.15 \text{ l} \\[1em]$

∴ Volume occupied = 6.15 l

Question 27

Which will have greater volume when the following gases are compared at S.T.P.

(a) 1.2 l N₂ at 25°C and 748 mm Hg

(b) 1.25 l O₂ at S.T.P.?

Answer

(a) 1.2 l N₂ at 25°C and 748 mm Hg

Initial conditions :

P₁ = Initial pressure of the gas = 748 mm Hg

V₁ = Initial volume of the gas = 1.2 l

T₁ = Initial temperature of the gas = 25°C = 25 + 273 = 298 K

Final conditions :

P₂ (Final pressure) = 760 mm of Hg

T₂ (Final temperature) = 273 K

V₂ (Final volume) = ?

By Gas Law:

$\dfrac{\text{P}_1\times\text{V}_1}{\text{T}_1} = \dfrac{\text{P}_2\times\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{748 \times 1.2}{298} = \dfrac{760 \times \text{V}_2}{273} \\[1em] \text{V}_2 = \dfrac{748 \times 1.2\times 273}{298 \times 760} \\[1em] \text{V}_2 = 1.081 \space l \\[1em]$

∴ Volume of N₂ at S.T.P. = 1.081 l and volume of O₂ at S.T.P. is 1.25 l. Hence, volume of O₂ at S.T.P. is greater than N₂ at S.T.P.

Question 28

50 cm³ of hydrogen is collected over water at 17°C and 750 mm Hg pressure. Calculate the volume of dry gas at S.T.P. The water vapour pressure at 17°C is 14 mm Hg.

Answer

Initial conditions :

P₁ = 750 - water vapour pressure = 750 - 14 = 736 mm Hg

V₁ = Initial volume of the gas = 50 cm³

T₁ = Initial temperature of the gas = 17°C = 17 + 273 = 290 K

Final conditions :

P₂ (Final pressure) = 760 mm of Hg

T₂ (Final temperature) = 273 K

V₂ (Final volume) = ?

By Gas Law:

$\dfrac{\text{P}_1\times\text{V}_1}{\text{T}_1} = \dfrac{\text{P}_2\times\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{736 \times 50}{290} = \dfrac{760 \times \text{V}_2}{273} \\[1em] \text{V}_2 = \dfrac{736 \times 50 \times 273}{290 \times 760} \\[1em] \text{V}_2 = 45.58 \text{ cm}^3 \\[1em]$

∴ Volume of dry gas = 45.6 cm³

Question 29

Calculate the volume of dry air at S.T.P. that occupies 28 cm³ at 14°C and 750 mm Hg pressure when saturated with water vapour. The vapour pressure of water at 14°C is 12 mm Hg.

Answer

Initial conditions :

P₁ = 750 - water vapour pressure = 750 - 12 = 738 mm Hg

V₁ = Initial volume of the gas = 28 cm³

T₁ = Initial temperature of the gas = 14°C + 273 = 287 K

Final conditions [S.T.P.] :

P₂ (Final pressure) = 760 mm of Hg

T₂ (Final temperature) = 273 K

V₂ (Final volume) = ?

By Gas Law:

$\dfrac{\text{P}_1\times\text{V}_1}{\text{T}_1} = \dfrac{\text{P}_2\times\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{738 \times 28 }{287} = \dfrac{760 \times \text{V}_2}{273} \\[1em] \text{V}_2 = \dfrac{738 \times 28 \times 273}{287 \times 760} \\[1em] \text{V}_2 = 25.86 \text{ cm}^3 \\[1em]$

∴ Volume of dry gas = 25.9 cm³

Question 30

L.P.G. cylinder can withstand a pressure of 14.9 atmosphere. The pressure gauge of the cylinder indicates 12 atmosphere at 27°C. Due to a sudden fire in the building the temperature rises. At what temperature will the cylinder explode?

Answer

P₁ = Initial pressure of the gas = 12 atm

T₁ = Initial temperature of the gas = 27°C = 27 + 273 = 300 K

P₂ = Final pressure of the gas = 14.9 atm

T₂ = Final temperature of the gas = ?

V₁ = V₂ = V [constant volume]

By Gas Law:

$\dfrac{\text{P}_1\times\text{V}_1}{\text{T}_1} = \dfrac{\text{P}_2\times\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{12\times\text{V}}{300} = \dfrac{14.9\times\text{V}}{\text{T}_2} \\[1em] \text{T}_2 = \dfrac{14.9 \times 300}{12}\\[1em] \text{T}_2 = 372.5 \text {K} \\[1em]$

∴ The temperature at which the cylinder will explode = 99.5°C.

Question 31

22.4 litres of a gas weighs 70 g at S.T.P. Calculate the weight of the gas if it occupies a volume of 20 litres at 27°C and 700 mm Hg of pressure.

Answer

Initial conditions :

P₁ = 700 mm Hg

V₁ = Initial volume of the gas = 20 litres

T₁ = Initial temperature of the gas = 27°C + 273 = 300 K

Final conditions [S.T.P.] :

P₂ (Final pressure) = 760 mm of Hg

T₂ (Final temperature) = 273 K

V₂ (Final volume) = ?

By Gas Law:

$\dfrac{\text{P}_1\times\text{V}_1}{\text{T}_1} = \dfrac{\text{P}_2\times\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{700 \times 20 }{300} = \dfrac{760 \times \text{V}_2}{273} \\[1em] \text{V}_2 = \dfrac{7 \times 2 \times 273}{3\times 76} \\[1em] \text{V}_2 = 16.76 \space l \\[1em]$

22.4 l of gas at S.T.P. weighs 70 g

∴ 16.76 l of gas at S.T.P. will weigh

= $\dfrac{70 \times 16.76}{22.4}$ = 52.38 g

∴ Weight of gas = 52.38 g

Numericals based on Boyle's law

Question 1

Volume of certain amount of a gas at 25°C and 100 cm Hg pressure is 80 mL. The gas is expanded to 160 mL keeping the temperature constant. Calculate the pressure of the expanded gas.

Answer

V₁ = Initial volume of the gas = 80 mL
P₁ = Initial pressure of the gas = 100 cm Hg
V₂ = Final volume of the gas = 160 mL
P₂ = Final pressure of the gas = ?

By Boyle's Law:

$\text{P}_1 \text{V}_1 = \text{P}_2 \text{V}_2$

Substituting the values :

$100 \times 80 = \text{P}_2 \times 160 \\[0.5em] \text{P}_2 = \dfrac{100}{2} \\[0.5em] \text{P}_2 = 50 \text{ cm of Hg }$

∴ Final pressure of the gas = 50 cm of Hg.

Question 2

At a particular temperature, a certain quantity of gas occupies a volume of 74 cm³ at a pressure of 760 mm. If the pressure is decreased to 740 mm, what will be the volume of the gas at the same temperature?

Answer

V₁ = Initial volume of the gas = 74 cm³
P₁ = Initial pressure of the gas = 760 mm
P₂ = Final pressure of the gas = 740 mm
V₂ = Final volume of the gas = ?

By Boyle's Law:

$\text{P}_1 \text{V}_1 = \text{P}_2 \text{V}_2$

Substituting the values :

$760 \times 74 = 740 \times \text{V}_2 \\[0.5em] \text{V}_2 = \dfrac{74 \times 760 }{740} \\[0.5em] \text{V}_2 = 76 \text{ cm}^3$

∴ Final volume of the gas = 76 cm³

Question 3

A student performed an experiment to measure pressure and volume of a gas at constant temperature and noted the following:

Calculate the value of x and y. Which law was used in the calculations? Draw graphs to show:

(i) volume plotted against pressure.

(ii) PV plotted against pressure

Answer

(a) V₁ = Initial volume of the gas = 80 cm³
P₁ = Initial pressure of the gas = 100 mm of Hg
P₂ = Final pressure of the gas = 125 mm of Hg
V₂ = Final volume = ?

By Boyle's Law:

$\text{P}_1 \text{V}_1 = \text{P}_2 \text{V}_2$

Substituting the values :

$100 \times 80 = 125 \times \text{V}_2 \\[0.5em] \text{V}_2 = \dfrac{100 \times 80 }{125} \\[0.5em] \text{V}_2 = 64 \text{ cm}^3$

∴ x = 64 cm³

(b) V₁ = Initial volume of the gas = 40 cm³
P₁ = Initial pressure of the gas = 200 mm of Hg
V₂ = Final volume of the gas = 32 cm³
P₂ = Final pressure of the gas = ?

By Boyle's Law:

$\text{P}_1 \text{V}_1 = \text{P}_2 \text{V}_2$

Substituting the values :

$200 \times 40 = \text{P}_2 \times 32 \\[0.5em] \text{P}_2 = \dfrac{200 \times 40 }{32} \\[0.5em] \text{P}_2 = 250 \text{ mm of Hg}$

∴ y = 250 mm of Hg

(i) Graph of volume plotted against pressure :

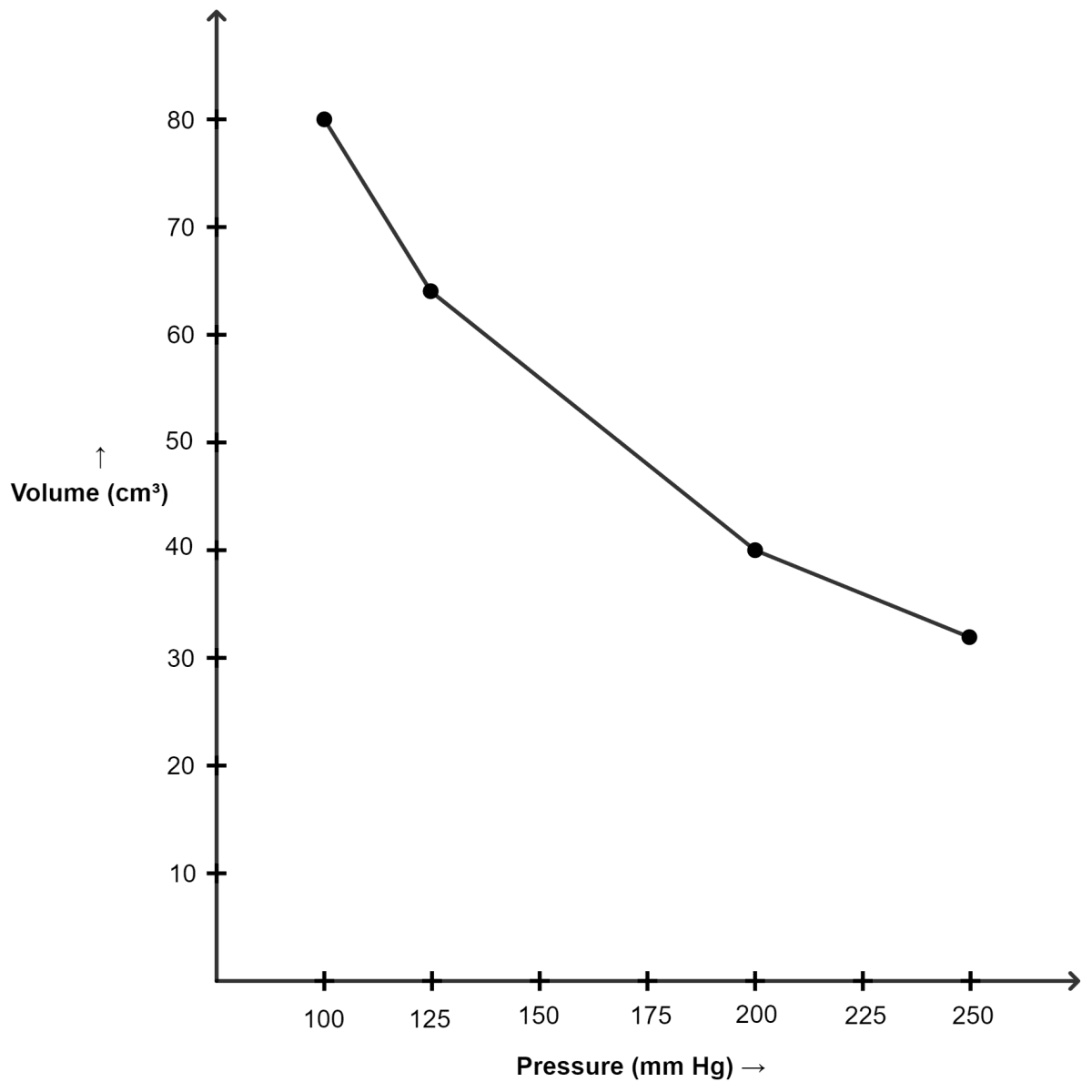
(ii) Graph of PV plotted against pressure :

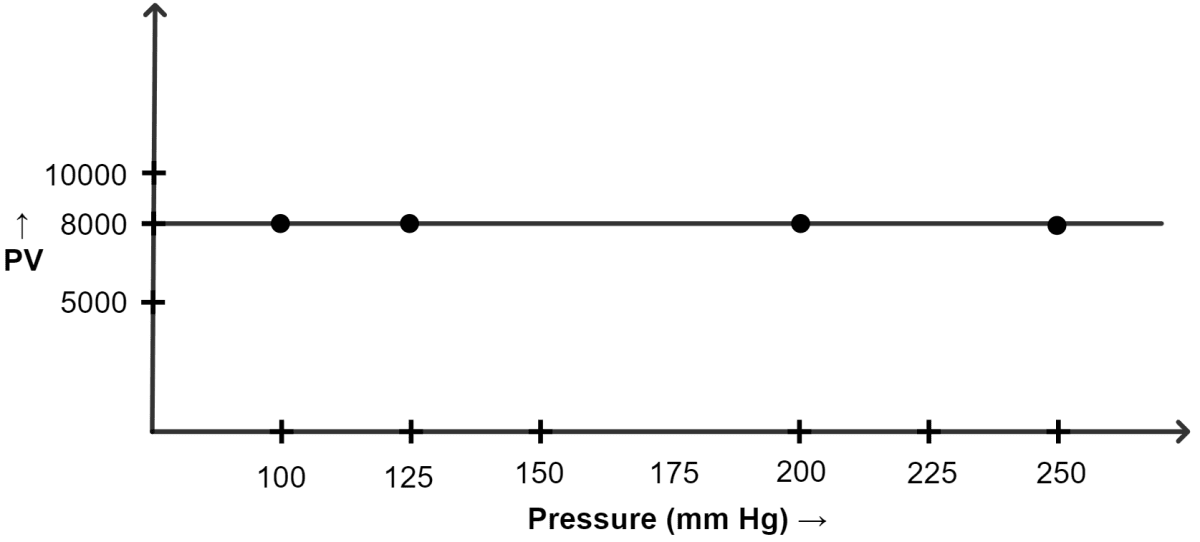
Question 4

At a constant temperature, volume of a gas was found to be 400 cm³ at a pressure of 760 mm Hg. If the pressure of the gas is increased by 25%, find the new volume.

Answer

V₁ = Initial volume of the gas = 400 cm³
P₁ = Initial pressure of the gas = 760 mm
P₂ = Final pressure of the gas

= increased by 25% of 760 mm Hg

= $\dfrac{25}{100}$ of 760 mm Hg

= ($\dfrac{1}{4}$ x 760) + 760

= 190 + 760 = 950 mm

V₂ = Final volume = ?

By Boyle's Law:

$\text{P}_1 \text{V}_1 = \text{P}_2 \text{V}_2$

Substituting the values :

$760 \times 400 = 950 \times \text{V}_2 \\[0.5em] \text{V}_2 = \dfrac{400 \times 760 }{950} \\[0.5em] \text{V}_2 = 320 \text{ cm}^3$

∴ Final volume = 320 cm³

Question 5

A vessel of capacity 600 cm³ contains hydrogen gas at a pressure of 330 cm Hg. What will be the pressure of hydrogen gas, when the vessel is connected to another vessel of 300 cm³ capacity ?

Answer

V₁ = Initial volume of the gas = 600 cm³
P₁ = Initial pressure of the gas = 330 cm Hg
V₂ = Final volume = 600 + 300 = 900 cm³
P₂ = Final pressure of the gas = ?

By Boyle's Law:

$\text{P}_1 \text{V}_1 = \text{P}_2 \text{V}_2$

Substituting the values :

$330 \times 600 = \text{P}_2 \times 900 \\[0.5em] \text{P}_2 = \dfrac{600 \times 330 }{900} \\[0.5em] \text{P}_2 = 220 \text{ cm of Hg}$

∴ Final pressure = 220 cm of Hg

Question 6

At constant temperature, a gas is at a pressure 1080 mm Hg. If the volume is decreased by 40%, find the new pressure of the gas.

Answer

V₁ = Initial volume of the gas = V

P₁ = Initial pressure of the gas = 1080 mm of Hg

V₂ = Final volume of the gas = decreased by 40%
= 60% of V₁ = $\dfrac{60}{100}$V = $\dfrac{3}{5}$V

P₂ = Final pressure of the gas = ?

By Boyle's Law:

$\text{P}_1 \text{V}_1 = \text{P}_2 \text{V}_2$

Substituting the values :

$\text{V} \times 1080 = \text{P}_2 \times \dfrac{3}{5}\text{V} \\[0.5em] \text{P}_2 = \dfrac{5\times 1080 }{3} \\[0.5em] \text{P}_2 = 1800 \text{ mm of Hg}$

∴ Final pressure = 1800 mm of Hg

Question 7

At constant temperature, the pressure of a gas is 940 mm of Hg. Calculate the pressure if the volume of the gas in decreased by 20%.

Answer

V₁ = Initial volume of the gas = V

P₁ = Initial pressure of the gas = 940 mm of Hg

V₂ = Final volume of the gas = decreased by 20%
= 80% of V₁ = $\dfrac{80}{100}$V = $\dfrac{4}{5}$V

P₂ = Final pressure of the gas = ?

By Boyle's Law:

$\text{P}_1 \text{V}_1 = \text{P}_2 \text{V}_2$

Substituting the values :

$\text{V} \times 940 = \text{P}_2 \times \dfrac{4}{5}\text{V} \\[0.5em] \text{P}_2 = \dfrac{5\times 940}{4} \\[0.5em] \text{P}_2 = 1175 \text{ mm Hg}$

∴ Final pressure = 1175 mm Hg

Question 8

If the pressure of 800 cm³ of a gas is tripled what will be the change in the volume?

Answer

V₁ = Initial volume of the gas = 800 cm³
P₁ = Initial pressure of the gas = P
P₂ = Final pressure of the gas = 3P
V₂ = Final volume of the gas = ?

By Boyle's Law:

$\text{P}_1 \text{V}_1 = \text{P}_2 \text{V}_2$

Substituting the values :

$\text{P} \times 800 = \text{V}_2 \times 3\text{P} \\[0.5em] \text{V}_2 = \dfrac{1}{3} \times 800 \\[0.5em]$

∴ Final volume is one-third of initial volume.

Numericals based on Charles' law

Question 1

Convert the following:

(i) 37 K to °C

(ii) 273 K to °C

(iii) -27°C to K

(iv) 27°C to K

Answer

(i) °C = Kelvin - 273 = 37 - 273 = -236°C

(ii) °C = Kelvin - 273 = 273 - 273 = 0°C

(iii) Kelvin = °C + 273 = -27 + 273 = 246 K

(iv) Kelvin = °C + 273 = 27 + 273 = 300 K

Question 2

20 mL of hydrogen gas at -13°C is heated to 117°C at constant pressure. Find the new volume of hydrogen.

Answer

V₁ = Initial volume of the gas = 20 mL
T₁ = Initial temperature of the gas = -13°C = -13 + 273 = 260 K
T₂ = Final temperature of the gas = 117°C = 117 + 273 = 390 K
V₂ = Final volume of the gas =?

By Charles' Law:

$\dfrac{\text{V}_1}{\text{T}_1} = \dfrac{\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{\text{20}}{260} = \dfrac{\text{V}_2}{390} \\[1em] \text{V}_2 = \dfrac{20 \times 390}{260} \\[1em] \text{V}_2 = 30 \text{ mL}$

∴ Final volume = 30 mL

Question 3

At what temperature in degree centigrade will the volume of a gas, which is originally at 0°C, double itself, pressure remaining constant?

Answer

V₁ = Initial volume of the gas = V
T₁ = Initial temperature of the gas = 0°C = 273 K
V₂ = Final volume of the gas = 2V
T₂ = Final temperature of the gas = ?

By Charles' Law:

$\dfrac{\text{V}_1}{\text{T}_1} = \dfrac{\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{\text{V}}{273} = \dfrac{2\text{V}}{\text{T}_2} \\[1em] \text{T}_2 = 2\times 273 \\[1em] \text{T}_2 = 546 \text{ K}$

∴ Final temperature in °C = 546 - 273 = 273°C

Question 4

Calculate the volume (in cm³) of air expelled from a vessel containing 0.4 litres of it at 250 K, when it is heated to 27°C at the same pressure.

Answer

1 lit = 1000 cm³
∴ 0.4 lit = 400 cm³

V₁ = Initial volume of the gas = 400 cm³
T₁ = Initial temperature of the gas = 250 K
T₂ = Final temperature of the gas = 27°C = 27 + 273 = 300 K
V₂ = Final volume of the gas = ?

By Charles' Law:

$\dfrac{\text{V}_1}{\text{T}_1} = \dfrac{\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{400}{250} = \dfrac{\text{V}_2}{300} \\[1em] \text{V}_2 = \dfrac{400 \times 300}{250} \\[1em] \text{V}_2 = 480 \text{ cm}^3$

Volume of air expelled = 480 - 400 = 80 cm³

Question 5

What will be the volume of a gas when 3 litres of it is cooled down from 27°C to -73°C at constant pressure?

Answer

V₁ = Initial volume of the gas = 3 litres
T₁ = Initial temperature of the gas = 27°C = 27 + 273 = 300 K
T₂ = Final temperature of the gas = -73°C = -73 + 273 = 200 K
V₂ = Final volume of the gas = ?

By Charles' Law:

$\dfrac{\text{V}_1}{\text{T}_1} = \dfrac{\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{3}{300} = \dfrac{\text{V}_2}{200} \\[1em] \text{V}_2 = \dfrac{3 \times 2}{3} \\[1em] \text{V}_2 = 2 \text{ lit}$

∴ Final volume = 2 litres.

Question 6

To what temperature must a gas at 300 K be cooled down in order to reduce its volume to $\dfrac{1}{3}$rd of its original volume, pressure remaining constant?

Answer

V₁ = Initial volume of the gas = V

T₁ = Initial temperature of the gas = 300 K

V₂ = Final volume of the gas = $\dfrac{1}{3}$V

T₂ = Final temperature of the gas = ?

By Charles' Law:

$\dfrac{\text{V}_1}{\text{T}_1} = \dfrac{\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{\text{V}}{300} = \dfrac{\dfrac{1}{3}\text{V}}{\text{T}_2} \\[1em] \text{T}_2 = \dfrac{300}{3} \\[1em] \text{T}_2 = 100 \text{ K}$

∴ Final temperature = 100 K

Question 7

Prove that the volume of a gas at 273°C is twice its volume at 273 K, at constant pressure.

Answer

V₁ = Initial volume of the gas = V

T₁ = Initial temperature of the gas = 273 K

T₂ = Final temperature of the gas = 273°C = 273 + 273 = 546 K

V₂ = Final volume of the gas = ?

By Charles' Law:

$\dfrac{\text{V}_1}{\text{T}_1} = \dfrac{\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{\text{V}}{273} = \dfrac{\text{V}_2}{546} \\[1em] \text{V}_2 = \dfrac{\text{V}\times 546}{273} \\[1em] \text{V}_2 = 2\text{V} \\[1em]$

∴ Volume of a gas at 273°C is twice its volume at 273 K

Question 8

A gas occupies 3 litres at 0°C. What volume will it occupy at -20°C pressure remaining constant?

Answer

V₁ = Initial volume of the gas = 3 litres

T₁ = Initial temperature of the gas = 0°C = 273 K

T₂ = Final temperature of the gas = -20°C = -20 + 273 = 253 K

V₂ = Final volume of the gas = ?

By Charles' Law:

$\dfrac{\text{V}_1}{\text{T}_1} = \dfrac{\text{V}_2}{\text{T}_2}$

Substituting the values :

$\dfrac{3}{273} = \dfrac{\text{V}_2}{253} \\[1em] \text{V}_2 = \dfrac{3 \times 253}{273} \\[1em] \text{V}_2 = 2.78 \text{ litres}$

∴ Final volume = 2.78 litres.